Рассмотрим общий случай, когда текстура проецируется на поверхность, которая затем проецируется на 2-х мерный экран. Мы проецируем проектором некое изображение на поверхность, а затем смотрим на нее из произвольной точки (см. рис.1). Т.е. снова проецируем изображение, на этот раз уже с поверхности на наблюдателя. При построении изображения эта ситуация моделируется крайне просто — проекция примитивов поверхности на экран дело обычное, а роль второй проекции (проецирование изображения на поверхность) играет привязка соответствующего места текстуры с изображением на примитивы.
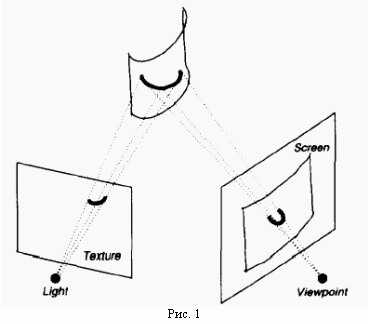
Нам осталось лишь научиться правильно привязывать текстуру с исходным изображением к нашей поверхности.
Всего мы имеем дело с четырьмя координатными системами.
1. Наблюдательская система ("clip" или "projection") — является обычным для графики 4-х координатным представлением 3-х мерного (объемного) пространства. Координаты зовутся x, y, z, w. Начало этой координатной системы лежит в точке наблюдения.
2. Экранная система ("screen") — 2-х мерный экран, который и видит наблюдатель. Эти координаты получаются из наблюдательской системы путём деления x и y на 
(индекс "s" у получающихся координат обозначает экранную систему).
3. Система источника света ("light") — это вторая объемная система координат 
. В начале этой системы координат находится источник света.
4. Текстурная система (texture) — координаты на плоскости проецируемой текстуры (тот слайд, сквозь который светит воображаемый источник света). Текстурные координаты получаются как 
(также можно вычислить 
, если мы решили не ограничиваться плоской текстурой).
Наша задача: имея точку 
на экране, нам необходимо найти соответствующую ей точку 
на текстуре.
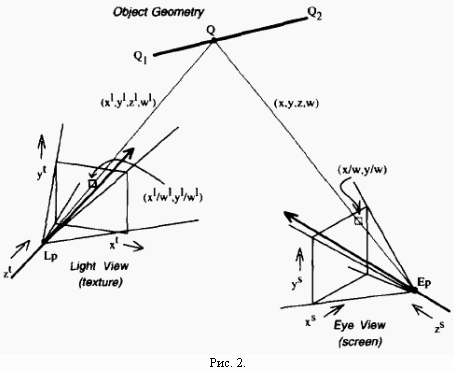
На рис. 2 показан сегмент линии в нашем трехмерном пространстве и его проекция на 2-х мерный экран. Этот сегмент — горизонтальная полоса сканирования на экране, расположенная между двумя рёбрами полигона. Координаты его концов в наблюдательской системе:
Нам необходимо найти координаты нашей произвольной точки отрезка в координатной системе источника света. Будем считать, что, так или иначе, мы уже определили координаты концов отрезка в системе источника света. Для начала нам необходимо найти параметр 
, соответствующий 
(в общем случае экранное 
наблюдательскому). Для этого запишем
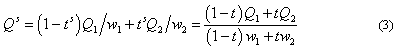
и решим относительно . Для тех, кому интересно, приведем все рассуждения:
Вычисление .
Зададим a и b, таким образом, что 
Зададим A и B так, что 
Тогда:
Легко проверить, что 
удовлетворяют этому уравнению, позволяя нам получить искомый параметр , и, далее, координаты 
.
Продолжим. У нас есть матрица M, переводящая координаты из системы источника в наблюдательскую:
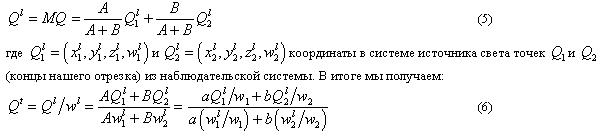
Уравнение (6) выражает координаты на поверхности текстуры, соответствующие любой точке сегмента выбираемой (линейно интерполируемой) параметром в экранных координатах.
Для того, чтобы получить координаты, мы должны линейно интерполировать 
Для каждого пикселя: 
Если 
постоянна на всём полигоне, то уравнение (7) приобретает вид
откуда мы имеем 
Здесь 
— текстурные координаты, синонимы 
Уравнение (8) и определяет текстурные координаты, которые можно привязать к вершинам передаваемого на ускоритель полигона. В более общем сложном случае проективной текстуры, выражаемом уравнением (7), требуется деление на 
, а не на 
.
