Завершаем разговор об алгоритмах шифрования, участвовавших в конкурсе NESSIE.
Алгоритм NUSH
Алгоритм NUSH, шифрующий данные 64-битными блоками, был описан в первой части статьи. Стоит сказать, что данный алгоритм (аналогично, например, известному алгоритму RC5) весьма легко преобразуется под другие размеры блока. На конкурс NESSIE, помимо 64-битного варианта, были представлены еще и варианты алгоритма, обрабатывающие 128-битные и 256-битные блоки данных [5].
128-битный вариант
Отличия 128-битного алгоритма NUSH от 64-битного состоят в следующем:
- Выполняется 17 раундов преобразований вместо 9.
- Блок данных делится на те же 4 субблока, но они имеют размер по 32-бита (а не по 16 бит). Соответственно, операции сложения и вычитания выполняются по модулю 232.
- Используются другие константы c (константы для модификации ключей, используемых в итерациях алгоритма) и s (число бит сдвига), а также другая последовательность логических операций #. Их значения сведены в следующую таблицу:
Раунд Итерация s c # 0 0 7 9B28A37B & 0 1 5 9DE5B521 | 0 2 15 0B8EE0D7 & 0 3 14 672AA715 | 1 0 3 0E356C9F | 1 1 30 BF54692A | 1 2 4 DC9E15C8 | 1 3 23 06D736E8 | 2 0 13 9263E8CF & 2 1 12 1FCD682D | 2 2 26 7368B074 | 2 3 16 2654F15A & 3 0 9 00EB3E4D | 3 1 28 18D62F6D & 3 2 8 632A557A | 3 3 18 1D953D21 | 4 0 23 CD4B2ACD | 4 1 8 49A0D3F4 | 4 2 26 C443FC66 & 4 3 4 E84C5BCB & 5 0 29 F750A732 & 5 1 16 2CDE9942 & 5 2 2 370C437A & 5 3 22 DA8B5654 | 6 0 23 99A76750 & 6 1 11 A1559437 | 6 2 26 9EA46718 | 6 3 13 83E984F8 | 7 0 20 AB5692E4 & 7 1 5 A6C5C46A | 7 2 28 25FB110E & 7 3 17 55955B2E & 8 0 19 FA639063 | 8 1 22 027E4DC6 | 8 2 6 919E96B2 & 8 3 25 62E96D0C | 9 0 12 AA7DE138 | 9 1 24 A674A66C & 9 2 27 B3F54983 | 9 3 10 AE29D0DB & 10 0 16 599470CB | 10 1 24 3B2E3FA0 & 10 2 9 A354CC6F & 10 3 13 516AF8C4 | 11 0 5 ADE11D33 | 11 1 10 860D95F2 & 11 2 26 BC2731A4 & 11 3 30 CCD12BAA & 12 0 9 BA518E95 & 12 1 16 22F7583A & 12 2 28 6C0A5FE8 & 12 3 24 8FAC2D74 & 13 0 27 D129E934 & 13 1 6 11DCE4C9 & 13 2 7 362F2F4A | 13 3 15 6CCB630D & 14 0 1 97919D88 | 14 1 13 823F95AC | 14 2 15 67C99A98 | 14 3 1 8E91D0CB & 15 0 23 AB796817 & 15 1 28 356459A7 & 15 2 12 668D9FA8 | 15 3 2 0D4DBF40 | 16 0 28 1ACCE5D8 & 16 1 14 F53B24C1 | 16 2 15 6DB89876 & 16 3 12 5C965DA5 | - Изменена процедура расширения ключа. В 128-битном алгоритме NUSH фрагменты исходного ключа K0...Kn-1 (n – размер ключа шифрования в 32-битных словах) используются в итерациях (ниже i – сквозной номер итерации, начиная с 0), а также в начальном и финальном преобразованиях следующим образом:
Применение Используемый фрагмент ключа (в зависимости от его размера) 128 бит 192 бита 256 бит KS0 K3 K2 K4 KS1 K2 K3 K5 KS2 K1 K4 K6 KS3 K0 K5 K7 KF0 K1 K5 K5 KF1 K0 K4 K4 KF2 K3 K3 K7 KF3 K2 K2 K6 KRi Ki mod n 256-битный вариант
256-битный вариант алгоритма, по сути, имеет те же отличия от 64-битного варианта:
- Количество раундов алгоритма увеличено до 33.
- Субблоки имеют размер по 64 бита, а операции сложения и вычитания выполняются по модулю 264.
- Используются другие константы c и s согласно следующей таблице:
Раунд Итерация s c 0 0 12 1A028E3B458FE65F 0 1 45 10CB1C5CAC3C7A75 0 2 7 0AA54C8D55CC6F5E 0 3 48 EE4AC8B12E2FC8D5 1 0 14 F787D15C240344D7 1 1 43 CACCAF60F2998693 1 2 8 4EA93E4DF9558E82 1 3 54 B57CDA0316BC1C92 2 0 49 623C7496C0D6FB68 2 1 47 BD7B065E84D852A9 2 2 37 A6CD2E5C6B1A30E7 2 3 55 788D9EFC078281B5 3 0 58 D0CF11A8FF9943E4 3 1 32 D04F01C7F3EA8E96 3 2 16 5313F574E5D1D2C8 3 3 36 DC8AB4437AAD50CF 4 0 13 66ED63D790921A4D 4 1 35 FA351C5183EBDA0B 4 2 50 DA694B14554D17C9 4 3 58 0A392FA5DE785CD1 5 0 21 75B1D5DE6561D08C 5 1 56 BC128DB2F22C591E 5 2 4 D19F06A961BC6E36 5 3 52 F3F2D208215DDA85 6 0 32 D9A5D482F930B1AF 6 1 19 FD98B3A189AD9851 6 2 28 B671A790FB204AE3 6 3 10 4E3B9DB2A290EC98 7 0 63 2CA2AFB114DF74A2 7 1 53 705CE63837B3616D 7 2 50 679D058EAL89A2EE 7 3 27 8398BAB59E3A506C 8 0 18 181F8AEFD8499AD4 8 1 40 17C41D9833728FE9 8 2 13 7E692E4DB9D09471 8 3 14 C900CDE6CB8AA557 9 0 8 EB2B8576C0419FE3 9 1 21 927C3FE32C9A2365 9 2 6 427410EB1EACBE4F 9 3 59 18A6FE2878B4D78D 10 0 17 436EB84357C5342F 10 1 5 1B94C23F94C24B3E 10 2 23 D3D831585E585A9C 10 3 10 F37E22A1587B9670 11 0 32 96A27FA6164197CD 11 1 20 C21BC4EAF449AC7E 11 2 53 BCCE8974A35A69D4 11 3 3 7FA98C9B495C2782 12 0 20 3B64D65041406FFB 12 1 42 AF82F6418C48F7DC 12 2 1 13B7D80A170E6AB6 12 3 58 09DFC1BBF5A51842 13 0 12 45B2F2934E2BECC4 13 1 30 F456D827335C90D3 13 2 38 7A2C6EE4672634D8 13 3 6 3AA0D9523BBBD398 14 0 23 D578F2AEA135F841 14 1 61 9A6635DA5227B8E9 14 2 7 F40F12A5B07BC3D8 14 3 12 BBD16B68649B4271 15 0 33 042753CE1B63F27B 15 1 41 A471D892D743F58D 15 2 17 B6CACF5958204C67 15 3 35 FB7786E2234AA30A 16 0 30 97EB25E4C9F33038 16 1 3 CD5D27E1802E58F4 16 2 60 0289FBE8CE5BD06A 16 3 55 26DBAA50CBC1E8B9 17 0 37 4116B2B8D89AFF86 17 1 50 1D658D6EEF814E49 17 2 12 A4B511D2427E3F73 17 3 41 E2A77BD9898E1326 18 0 7 65DEA88074B941FD 18 1 40 8E55B0DC3CEE4398 18 2 35 C14E2ADD6601EBDC 18 3 45 A24F31D25E456E34 19 0 2 AD83615AC0E7AEAE 19 1 44 81FCC39F84A54A8B 19 2 4 D15C7E21FE235136 19 3 49 5F5AC08E5A961B43 20 0 29 0CEC9543F2A66676 20 1 12 7C034EBA929A8B8E 20 2 56 C0F4CE12EC988EBB 20 3 18 5D358844AE5699F9 21 0 59 42E8D74DB4919B52 21 1 21 8250D178F5557F8A 21 2 45 532394E648E4F3FC 21 3 60 3E2BF92B03691AD8 22 0 12 FA9268E710647D5B 22 1 62 BBD56F8408E2E651 22 2 59 793C3027EB0C5B8C 22 3 51 7643D2BB11326B87 23 0 20 4B9FF22BB56211E4 23 1 42 AA39E9382F34B664 23 2 6 E212D331BFE06A72 23 3 27 1755736EA478F948 24 0 1 59CA19F718A53EAA 24 1 17 F44B30FA21C0A6ED 24 2 24 71F47E295DA0855C 24 3 51 5036E2EE9C4166B9 25 0 32 6D32721CF1269E70 25 1 4 C51E826355EC445F 25 2 26 0E8E66931EF37C41 25 3 46 9A94B3039660D3DE 26 0 2 1ED158ECD9D68529 26 1 1 0ECE52DC8F1C3952 26 2 38 86A20A1FFFC847E5 26 3 12 FF1DADC90C09A612 27 0 7 B896156E08C55F6D 27 1 41 644DEA351C86F456 27 2 45 29B4B572556F360D 27 3 37 875399911A5A79D1 28 0 24 32EC6F05BC921BA5 28 1 10 CE0FB52C15C61A97 28 2 4 7F4E15212953F03D 28 3 2 873CA0565BBEC3E8 29 0 6 CDF1B94C29B3812F1 29 1 18 AAAEA6E308E92F68 29 2 9 703CCA8345EC51FC 29 3 52 4618BB1B1B33EF0C 30 0 8 F039732AAD11FE46 30 1 57 86D89114CE8DE23F 30 2 1 330AEDC7E44B8AF0 30 3 31 96D7869EDD33E500 31 0 35 F59CC3B1E9354045 31 1 33 AD3DB4F4A1AA8433 31 2 11 724ECE1C833975EA 31 3 16 98516AB5C5303E6E 32 0 6 ACF4FD043B90CCB6 32 1 13 8D8A1DA51BE5CEC1 32 2 15 11D0127B77B9427B 32 3 45 67C2DE1924CAA5ED Что касается логических операций #, то они выполняются в той же последовательности, что и для 128-битного алгоритма. В раундах, которые отсутствуют в 128-битном варианте, используются операции согласно следующему правилу:
#i = #i mod 64,где i – сквозной номер итерации.
- Фрагменты исходного ключа используются в преобразованиях алгоритма согласно следующей таблице (в данном случае ключ делится на 64-битные слова):
Применение Используемый фрагмент ключа (в зависимости от его размера) 128 бит 192 бита 256 бит KS0 K1 K2 K3 KS1 K0 K1 K2 KS2 K1 K0 K1 KS3 K0 K2 K0 KF0 K0 K1 K2 KF1 K1 K2 K3 KF2 K0 K2 K0 KF3 K1 K0 K1 KRi Ki mod n
Криптоанализ алгоритма
Против 128- и 256-битных вариантов алгоритма NUSH применима та же атака, что и против 64-битного варианта [11]. Атака, предложенная китайскими учеными Ву Венлинг (Wu Wenling) и Фенг Денггуо (Feng Dengguo), позволяет методом линейного криптоанализа вычислить, например, 256-битный ключ 128-битного варианта алгоритма при наличии 2126 известных открытых текстов выполнением 264 операций шифрования. Аналогичные атаки существуют и для 256-битного варианта, и для других размеров ключей.
Поскольку данные атаки говорят о недостаточном запасе криптостойкости алгоритма NUSH, 192- и 256-битные варианты алгоритма также не вышли во второй раунд конкурса NESSIE [8].
Алгоритм Q
Так же, как и рассмотренные в прошлой части алгоритмы Anubis и Grand Cru, алгоритм Q наследует структуру и часть преобразований от алгоритма Rijndael. Соответственно, алгоритм представляет 128-битный блок данных в виде байтового массива 4 * 4, над которым и выполняются преобразования.
Алгоритм, теоретически, не ограничивает размер используемых ключей шифрования ни сверху, ни снизу. Однако, в рамках конкурса NESSIE рассматривалось только три фиксированных размера ключа: 128, 192 и 256 бит.
Автор алгоритма – Лесли МакБрайд (Leslie McBride) из компании Mack One Software (США). На конкурс NESSIE была представлена версия 2.0 алгоритма Q, которая и описана ниже.
Стоит отметить, что спецификация алгоритма Q [6], по сравнению, например, с подробнейшими описаниями рассмотренных в этой части статьи алгоритмов NUSH [5] и SC2000 [10], недостаточно детально описывает данный алгоритм. Кроме того, некоторые эксперты (см., например, [4]) отмечают наличие противоречий в данной спецификации. Поэтому ниже приведено лишь краткое описание алгоритма Q.
Структура алгоритма
В каждом раунде алгоритма выполняются следующие операции [6]:
- Первое наложение ключа (операция KA). Выполняется побитовой логической операцией «исключающее или» (XOR), которая применяется к каждому биту обрабатываемого блока и соответствующему биту фрагмента расширенного ключа для данной операции.
- Первая табличная замена BS1. Используемая здесь таблица взята в неизменном виде из алгоритма Rijndael, как и таблица замен алгоритма Grand Cru. Данная таблица приведена в предыдущей части статьи.
- Второе наложение ключа (операция KB). Аналогично KA, наложение выполняется с помощью операции XOR.
- Вторая табличная замена BS2. Данная операция унаследована от алгоритма Serpent, подробно описанного в [12].
- Третье наложение ключа (операция KN). Отличие данной операции от KA и KB состоит в том, что они используют один и тот же фрагмент расширенного ключа во всех раундах, тогда как подключ, используемый в операции KN, уникален для каждого раунда алгоритма.
- Операция CS – побайтный циклический сдвиг каждого (кроме первого) столбца массива данных. j-й столбец массива сдвигается на j бит вверх.
- Третья табличная замена BS3. Также унаследована от алгоритма Serpent.
Количество раундов R алгоритма определено в его описании [6] как 8 для обычных применений или 9 в случаях, когда требуется усиленная защита.
Общая структура алгоритма такова:
- Сначала выполняется предварительное отбеливание, т.е. наложение на данные фрагмента ключа для предварительного отбеливания, которое выполняется абсолютно аналогично операции KA.
- Затем выполняется R описанных выше раундов преобразований.
- Наконец, выполняется заключительное преобразование, состоящее из последовательно выполняемых операций KA, BS1 и KB, после чего выполняется финальное отбеливание. Финальное отбеливание аналогично предварительному, за исключением того, что в нем используется другой фрагмент ключа.
Расшифрование выполняется практически аналогично зашифрованию, за исключением следующего:
- При расшифровании меняются местами операции KN и CS.
- Используются инверсные таблицы замен.
- Раундовые ключи используются в обратной последовательности.
Криптоанализ алгоритма
Результаты исследований алгоритма Q в рамках конкурса NESSIE оказались весьма неутешительными: алгоритм подвержен как дифференциальному [1, 2], так и линейному криптоанализу [4]. Поэтому Q не был выбран во второй раунд конкурса [7].
Алгоритм SC2000
Алгоритм SC2000 разработан в 2000 г. группой японских специалистов из компании Fujitsu и Университета г. Токио.
SC2000 имеет три фиксированных размера ключа шифрования: 128, 192 и 256 бит.
Структура алгоритма
Алгоритм представляет собой SP-сеть; в нем выполняется 7 раундов преобразований при использовании 128-битного ключа или 8 раундов при использовании ключей больших размеров. Раунд алгоритма имеет достаточно сложную структуру; первый раунд показан на рис. 1.
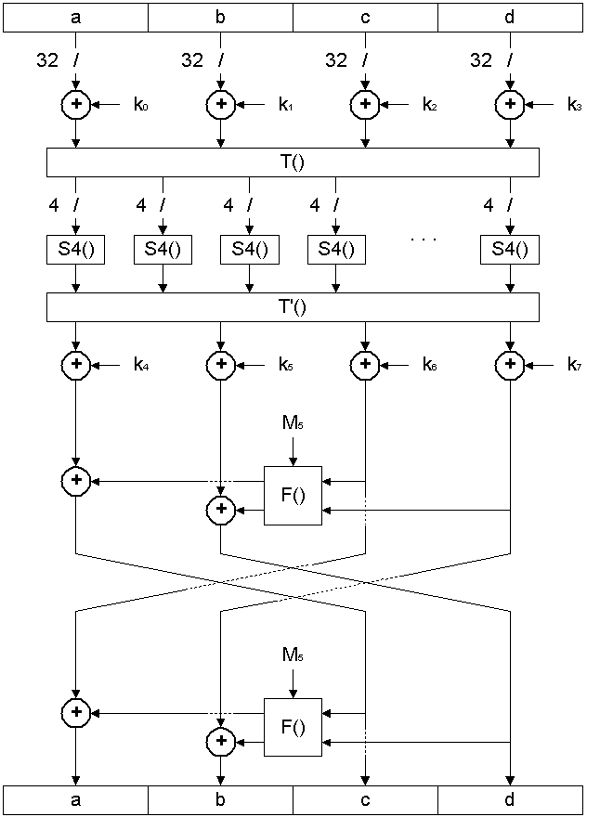Рис. 1. 1-й раунд алгоритма SC2000В нем выполняются следующие операции [10]:
- Входное 128-битное значение делится на 4 субблока по 32 бита, на каждый из которых операцией XOR накладывается соответствующий 32-битный фрагмент расширенного ключа (процедура расширения ключа будет описана ниже), в данном случае – фрагменты k0...k3.
- Затем выполняется операция T(), которая переразбивает блок данных на 32 субблока по 4 бита каждый. Переразбиение выполняется так (см. рис. 2):
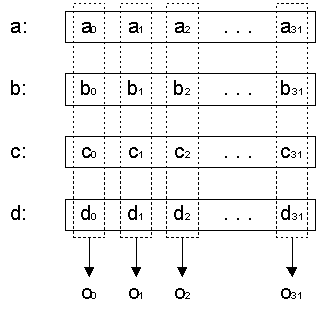Рис. 2. Операция T() алгоритма SC2000i-й 4-битный субблок (обозначим его oi) формируется из четырех i-х бит субблоков a, b, c и d. - Каждый 4-битный субблок «прогоняется» через таблицу замен S4, которая заменяет входное 4-битное значение выходным того же размера согласно следующей таблице:
2 5 10 12 7 15 1 11 13 6 0 9 4 8 3 14 т.е., значение 0 заменяется значением 2, 1 меняется на 5 и т.д.
- Обрабатываемый блок данных снова переразбивается на 32-битные субблоки с помощью операции T’(), которая, фактически, является обратной к операции T() – см. рис. 3 (на рисунке 4-битные субблоки обозначены как t0...t31).
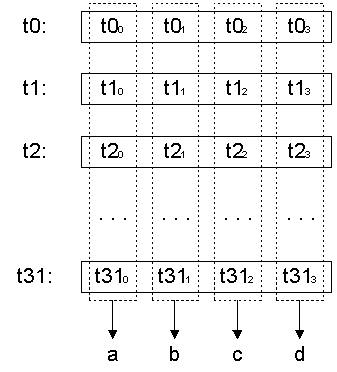Рис. 3. Операция T’() алгоритма SC2000 - Выполняется наложение операцией XOR еще четырех фрагментов расширенного ключа; для первого раунда – это фрагменты k4...k7.
- Значения субблоков C и D (а также маскирующая константа M5 = 555555552) подаются на вход функции F(), которая будет подробно описана ниже. В результате выполнения данной функции получаются два 32-битных значения, которые накладываются операцией XOR на субблоки A и B.
- Субблоки A и B меняются местами, соответственно, с субблоками C и D, после чего повторно выполняется шаг 6.
Упомянутая выше функция F() обрабатывает два входных 32-битных субблока следующим образом (см. рис. 4):
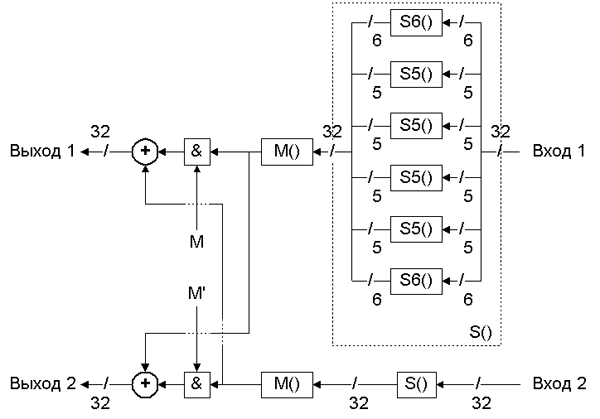Рис. 4. Функция F() алгоритма SC2000- Каждое из входных 32-битных значений разбивается на 6 фрагментов, два из которых являются 6-битными, а остальные имеют размер по 5 бит.
- 6-битные фрагменты прогоняются через таблицу замен S6, а 5-битные обрабатываются таблицей S5. Таблица S6 выглядит так:
47 59 25 42 15 23 28 39 25 38 36 19 60 24 29 56 37 63 20 61 55 2 30 44 9 10 6 22 53 48 51 11 62 52 35 18 14 46 0 54 17 40 27 4 31 8 5 12 3 16 41 34 33 7 45 49 50 58 1 21 43 57 32 13 S5 определена следующим образом:
20 26 7 31 19 12 10 15 22 30 13 14 4 24 9 18 27 11 1 21 6 16 2 28 23 5 8 3 0 17 29 25 Принцип действия данных таблиц аналогичен S4.
- Полученные после замены значения снова объединяются в 32-битные субблоки, каждый из которых обрабатывается операцией M(); данная операция выполняет умножение 32-битного входного значения (представленного в виде вектора) на матрицу размером 32 х 32 бит, которая определена следующим образом :
D0C19225 A5A2240A 1B84D250 B728A4A1 6A704902 85DDDBE6 766FF4A4 ECDFE128 AFD13E94 DF837D09 BB27FA52 695059AC 52A1BB58 CC322F1D 1844565B B4A8ACF6 34235438 6847A851 E48C0CBB CD181136 9A112A0C 43EC6D0E 87D8D27D 487DC995 90FB9B4B A1F63697 FC513ED9 78A37D93 8D16C5DF 9E0C8BBE 3C381F7C E9FB0779 - На первое из 32-битные значений, полученных после обработки субблоков операцией M(), логической побитовой операцией «и» (&) накладывается маскирующая константа (на рис. 4 обозначенная M). На второе значение аналогичным образом накладывается константа M’ – побитовый комплемент к M.
- Два выходных значения (обозначим их Out1 и Out2) получаются в результате следующих действий: Out1 = (V1 & M)
V2,
Out2 = (V2 & M’) V1,где V1 и V2 – значения, полученные после обработки 32-битных субблоков операцией M().
Как было сказано выше, в алгоритме выполняется 7 раундов преобразований при использовании 128-битных ключей или 8 раундов, если используются ключи размером 192 или 256 бит. В каждом раунде используется по 8 различных 32-битных фрагментов расширенного ключа. Раунды незначительно различаются между собой в следующем:
- В каждом четном раунде (считая, что раунды нумеруются с 1-го) вместо описанной выше маскирующей константы M5 используется константа M3 = 33333333 (шестнадцатеричное значение).
- В последнем раунде не выполняются шаги 6 и 7 описанной выше последовательности действий для первого раунда.
Расшифрование
Расшифрование данных алгоритмом SC2000 весьма похоже на зашифрование, за исключением следующих отличий:
- Фрагменты расширенного ключа применяются в обратной последовательности, т.е. в первом раунде (при использовании 128-битного ключа) операцией XOR накладываются сначала подключи k52...k55, а затем – k48...k51 и т.д. в следующих раундах расшифрования.
- Маскирующие константы используются в обратной последовательности, т.е. M3 в нечетных раундах и M5 – в четных.
- Вместо таблицы S4 используется обратная ей таблица, которая выглядит следующим образом:
10 6 0 14 12 1 9 4 13 11 2 7 3 8 15 5
Расширение ключа
Расширение ключа выполняется в два этапа: сначала на основе ключа шифрования вычисляется промежуточный ключ, после чего из промежуточного ключа вычисляется требуемое количество фрагментов расширенного ключа.
Прежде всего, ключ шифрования используется для инициализации начального ключевого массива uk0...uk7 следующим образом:
- 256-битный ключ просто разбивается на 32-битные фрагменты uk0...uk7;
- 192-битный ключ делится на фрагменты uk0...uk5, два остальных фрагмента инициализируются так: uk6 = uk0;
uk7 = uk1. - 128-битный ключ разбивается на фрагменты uk0...uk3, фрагменты uk4...uk7 эквивалентны фрагментам uk0...uk3.
Затем вычисляется набор промежуточных ключей: a0...a2, b0...b2, c0...c2 и d0...d2. Все они вычисляются с помощью процедуры генерации промежуточных ключей, показанной на рис. 5.
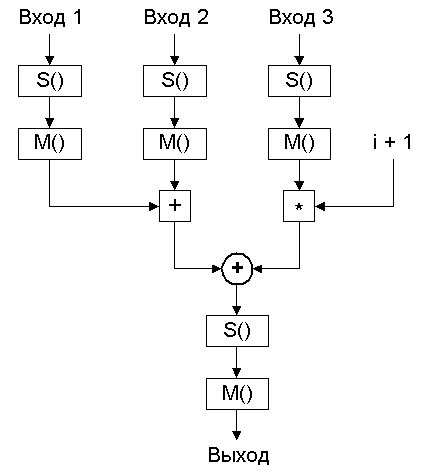Рис. 5. Процедура генерации промежуточных ключей алгоритма SC2000Данная процедура повторяется 12 раз по количеству вычисляемых промежуточных ключей. Входные и выходные параметры данной процедуры определяются согласно следующей таблице:
Вход 1 Вход 2 Вход 3 Выход 4 * i uk0 uk1 ai, i = 0, 1, 2 4 * i + 1 uk2 uk3 bi, i = 0, 1, 2 4 * i + 2 uk4 uk5 ci, i = 0, 1, 2 4 * i + 3 uk6 uk7 di, i = 0, 1, 2 Для каждой группы промежуточных ключей в цикле по i = 0...2 процедура выполняет следующие действия:
- Каждый из трех входов обрабатывается функцией S(), которая осуществляет «прогон» 32-битного фрагмента данных через описанные выше таблицы замен S5 и S6 – см. рис. 4.
- Результаты предыдущего шага обрабатываются описанной выше функцией M().
- Первый из фрагментов, полученных на предыдущем шаге (т.е. результат обработки функциями S() и M() первого входа), складывается со вторым по модулю 232.
- Третий из фрагментов, полученных на шаге 2, умножается на значение i + 1 по модулю 232.
- Результаты шагов 3 и 4 объединяются операцией XOR.
- Результат предыдущего шага обрабатывается функцией S(), а затем – функцией M(), в результате чего получается выходное значение.
После этого из промежуточного ключа вычисляются фрагменты расширенного ключа выполнением в цикле по n от 0 до 55 (для 192- и 256-битных ключей шифрования – в цикле от 0 до 63) процедуры, показанной на рис. 6. В качестве входных значений процедура берет 4 различных фрагмента промежуточного ключа (будет описано ниже), над которыми выполняются следующие действия:
- 1-е входное значение циклически сдвигается влево на 1 бит.
- Аналогично сдвигается 3-е входное значение.
- Результат шага 1 складывается со вторым входным значением по модулю 232.
- Из результата шага 2 вычитается модулю 232 четвертое входное значение.
- Результат предыдущего шага циклически сдвигается влево на 1 бит.
- Результаты шагов 3 и 5 объединяются операцией XOR, что и дает выходное значение.
Выходным значением данной процедуры является n-й 32-битный фрагмент расширенного ключа. Входные значения определяются следующими таблицами, первая из которых определяет группу промежуточных ключей (т.е. ai, bi, ci или di), из которой берется конкретное входное значение:
t Вход 1 Вход 2 Вход 3 Вход 4 0 ai bi ci di 1 bi ai di ci 2 ci di ai bi 3 di ci bi ai 4 ai ci di bi 5 bi di ci ai 6 ci ai bi di 7 di bi ai ci 8 ai di bi ci 9 bi ci ai di 10 ci bi di ai 11 di ai ci bi Параметр t определяется из n следующим образом:
t = (n +
n / 36
) mod 12.Вторая таблица определяет индекс i фрагмента промежуточного ключа для конкретного входа:
n mod 9 Вход 1 Вход 2 Вход 3 Вход 4 0 0 0 0 0 1 1 1 1 1 2 2 2 2 2 3 0 1 0 1 4 1 2 1 2 5 2 0 2 0 6 0 2 0 2 7 1 0 1 0 8 2 1 2 1 Криптоанализ алгоритма
Алгоритм SC2000 не вышел во второй раунд конкурса NESSIE – с одной стороны, у алгоритма достаточная криптостойкость (известны лишь методы вскрытия вариантов алгоритма SC2000 с уменьшенным числом раундов – например, описанные в [3] и [9]) и неплохое быстродействие. С другой стороны, алгоритм имеет весьма сложную структуру, преимущества которой недостаточно убедительно обоснованы в спецификации алгоритма. Опасаясь скрытых слабостей и возможных недокументированных особенностей алгоритма, эксперты не выбрали данный алгоритм во второй раунд [7].
Заключение
Здесь были описаны только те алгоритмы-участники конкурса NESSIE, которые не вышли в его финал. Примерно столько же алгоритмов блочного симметричного шифрования вышло в финал конкурса, где в условиях жесткой конкуренции было выбрано несколько победителей конкурса. Однако, все это – тема отдельной статьи.
- Biham E., Dunkelman O., Furman V., Mor T. Preliminary Report on the Nessie Submissions: Anubis, Camellia, Khazad, IDEA, Misty1, NIMBUS, and Q. // http://www.cosic.esat.kuleuven.be. – Technion, Haifa, Israel.
- Biham E., Furman V., Misztal M., Rijmen V. Differential Cryptanalysis of Q. // http://citeseer.ist.psu.edu. – February 11, 2001.
- Dunkelman O., Keller N. Boomerang and Rectangle Attacks on SC2000. // http://citeseer.ist.psu.edu. – July 3, 2001.
- Keliher L., Meijer H., Tavares S.E. High Probability Linear Hulls in Q. // http://www.cosic.esat.kuleuven.be.
- Lebedev A.N., Volchkov A.A. NUSH. Cryptographic Algorithms Based upon the Block Cipher Called «NUSH». // http://www.cosic.esat.kuleuven.be. – LAN Crypto, Int., Moscow, Russia.
- McBride L. Q – A Proposal for NESSIE. v2.00. // http://www.cosic.esat.kuleuven.be – Mack One Software, Galveston, USA.
- Preneel B., Bosselaers A., Ors S.B., Biryukov A., Granboulan L., Dottax E., Murphy S., Dent A., White J., Dichtl M., Pyka S., Serf P., Biham E., Barkan E., Dunkelman O., Ciet M., Sica F., Knudsen L., Raddum H. NESSIE Public Report D18: Update on the selection of algorithms for further investigation during the second round. // http://www.cosic.esat.kuleuven.be. – Version 1.0 – March 11, 2002.
- Preneel B., Van Rompay B., Granboulan L., Martinet G., Murphy S., Shipsey R., White J., Dichtl M., Serf P., Schafheutle M., Biham E., Dunkelman O., Ciet M., Quisquater J-J., Sica F., Knudsen L., Raddum H. NESSIE Phase I: Selection of Primitives. // http://www.cryptonessie.org. – 23 September 2001.
- Raddum H., Knudsen L.R. A Differential Attack on Reduced-Round SC2000. // http://citeseer.ist.psu.edu. – University of Bergen – 30th April 2001.
- Shimoyama T., Yanami H., Yokoyama K., Takenaka M., Itoh K., Yajima J., Torii N., Tanaka H. Specification and Supporting Document of the Block Cipher SC2000. // http://www.cosic.esat.kuleuven.be – 2000.
- Wenling W., Dengguo F. Linear cryptanalysis of NUSH block cipher. // http://www.scichina.com – Chinese Academy of Sciences – 2002.
- Панасенко С.П. Алгоритмы шифрования – финалисты конкурса AES. Часть 1. // iXBT.com. – http://www.ixbt.com/soft/alg-encryption-aes.shtml – 24.08.2006 г.
