За последние несколько лет трехмерная компьютерная графика сделала гигантский шаг вперед. Качество и реалистичность, казавшиеся невозможными раньше, сейчас реализуются графическими ускорителями, доступными самому широкому кругу пользователей. Однако, принципы создания и визуализации трехмерных сцен и объектов практически не изменились. Базовым графическим примитивом по прежнему является треугольник. Каждый объект сцены разбивается на треугольники и в таком виде хранится и выводится на экран. Недостатки такого подхода очевидны: сложные объекты получаются либо слишком угловатыми, либо содержат огромное количество мелких треугольников, что приводит к существенному падению производительности. Таким образом, разработчикам и дизайнерам компьютерных игр приходится постоянно делать выбор между скоростью и качеством. Надо сказать, что разработано множество способов, позволяющих улучшить качество при минимальных вычислительных затратах, но даже они не способны скрыть угловатую сущность треугольника.
Почему бы тогда не отказаться от плоского треугольника в пользу более криволинейных геометрических примитивов? Дело в том, что использование кривых поверхностей в общем случае приводит к необходимости производить большое количество операций с вещественными числами. Такие примитивы используются в профессиональной трехмерной графике, но в системах визуализации в реальном времени (компьютерных играх) они не применимы в силу своей вычислительной сложности. Хотя и в этом направление ведутся работы, например в этой статье предлагается в качестве примитивов использовать квадрики с функциями возмущения, что позволяет создавать сложные формы объектов, используя минимум примитивов. Тем не менее, мне кажется, что в ближайшее время не стоит ожидать появления широко доступных графических ускорителей, способных обеспечить достаточно высокую скорость отрисовки подобных поверхностей. 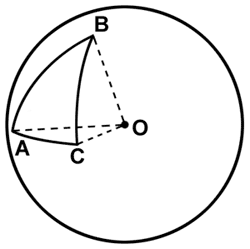
В качестве альтернативы плоским треугольникам и сложным криволинейным функциям, я предлагаю рассмотреть такие графические примитивы, как сферические треугольники.
Сферический треугольник — это три точки на сфере, соединенные дугами большого круга. Наиболее интересны эйлеровы сферические треугольники — это те, что полностью лежат в одном полушарии. С одной стороны, они уже не являются плоскими объектами, а с другой — могут быть легко заданы тремя вершинами и радиусом окружности, на которой они лежат (радиусом кривизны). На самом деле это задание не однозначно — треугольник может быть как выпуклым, так и вогнутым. Будем считать, что треугольник с положительным радиусом кривизны — выпуклый, с отрицательным — вогнутый.
Использование сферических треугольников вместе с плоскими треугольниками дает множество преимуществ: 
- Более реалистичные объекты. Существует большое количество поверхностей, которые могут быть смоделированы несколькими сферическими треугольниками, тогда как число плоских треугольников, необходимых для построения модели такого же качества, может исчисляться тысячами. Кроме того, при приближении камеры к объекту, он не будет распадаться на грани, останется гладким. Справедливости ради нужно отметить, что возникают другие проблемы — сложность стыковки простых и сферических треугольников, сложность стыковки сферических треугольников разного радиуса. Тем не менее, во многих случаях эти проблемы могут быть решены.
- Хорошая совместимость с существующими системами. Сферический треугольник, также как и плоский, задается тремя вершинами. Радиус кривизны нужен только на последней стадии вывода на экран. При проведении предварительной обработки, например при расчете геометрии, кривизну можно не учитывать.
- Высокая скорость отрисовки. Благодаря относительной простоте, большая часть вычислений может быть произведена в целых числах. Это позволяет выводить сцену на экран с очень высокой скоростью. Например, на компьютере Celeron-500 "летающая тарелка" с иллюстрации выводилась со скоростью 60 fps в движении, без аппаратной 3D-акселерации.
Иллюстрации к этой статье были отрендерены в специально написанной демонстрационной программе. Эта программа читает информацию о сцене из текстового файла, указанного в качестве параметра. Таким образом, можно создавать свои собственные сцены. Только нужно учесть, что эта программа не умеет выводить плоские треугольники — только сферические. Хотя сферический треугольник с большим радиусом кривизны вполне может сойти за плоский.
Проекция сферического треугольника на картинную плоскость с наложением текстуры
Будем считать, что нам известны следующие параметры сферического треугольника:
- Координаты трех вершин (Ax, Ay, Az), (Bx, By, Bz), (Cx, Cy, Cz).
- Радиус кривизны R.
- Текстурные координаты вершин (Au, Av), (Bu, Bv), (Cu, Cv).
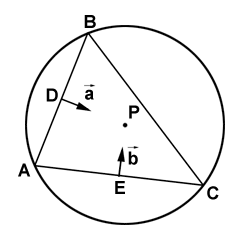
Прежде всего, нужно найти центр сферы, на которой лежит этот треугольник.
Для этого, рассмотрим плоскость, в которой лежат все три вершины A, B, C треугольника. Пересечение сферы и плоскости дает окружность, которая является описанной вокруг треугольника окружностью. Ее центр P лежит в точке пересечения срединных перпендикуляров и может быть найден по следующей формуле:
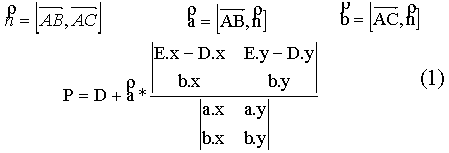
где
- D — середина отрезка AB;
- E — середина отрезка AC;
- n — нормаль к плоскости треугольника.
- a — срединный перпендикуляр к стороне AB.
- b — срединный перпендикуляр к стороне AC.
Если детерминант в знаменателе равен нулю, его можно заменить на такой же, но с другой парой координат — (y, z) или (x, z). Один из них будет неравен нулю хотя бы потому, что векторное произведение a и b ненулевой вектор.
Вектор с началом в центре сферы O и концом в центре окружности P коллинеарен вектору нормали n. Таким образом, мы получаем прямоугольный треугольник APO, гипотенуза и один катет которого известны. Это позволяет найти точку O по следующей формуле:

От знака перед корнем в этой формуле зависит будет треугольник выпуклым или вогнутым. Мы договорились, что выпуклость/вогнутость будет задаваться знаком радиуса, именно в этом месте он и играет роль.
Центр сферы достаточно найти только один раз — в дальнейшем, нужно лишь применять к нему те же трансформации, что и к вершинам. 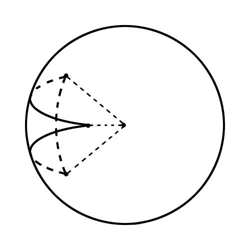
Предположим, что геометрию мы рассчитали и теперь нужно вывести сферический треугольник на картинную плоскость. Прежде всего, полезно определить видим ли он вообще. Плоский треугольник считается видимым, если его нормаль направлена в сторону картинной плоскости. Со сферическими треугольниками все немного сложнее. Сферический треугольник видим, если хотя бы один из векторов OA, OB, OC направлен в сторону картинной плоскости.
После проверки на видимость, сферический треугольник нужно спроецировать на картинную плоскость. Будем считать, что она совпадает с плоскостью z = 0, а проектирующие прямые параллельны оси Oz.
Процесс проецирования организуем следующим образом — просканируем все пиксели окна вывода картинной плоскости и для каждого определим цвет, если он лежит внутри сферического треугольника. На самом деле, существуют методы, позволяющие обойтись без сканирования всего окна вывода, ограничиться только пикселями, лежащими внутри границ треугольника. Проблема тут в том, что границы — это эллиптические кривые. Упомянутая выше демонстрационная программа реализует один из этих методов, причем с довольно высокой скоростью. Но этот способ довольно сложен и относится скорее к методам программной оптимизации, поэтому я оставлю его за рамками этой статьи. Будем считать, что сканируется все окно вывода.
Получив координаты (x, y) пикселя, нужно найти z координату точки X на сфере, проецирующейся в этот пиксель. Это можно сделать пользуясь следующей формулой:
Если выражение под корнем меньше нуля, то в данный пиксель не проектируется ни одна точка сферы. Если равно нулю, то существует только одна такая точка. Если больше нуля, то таких точки две — на внешней поверхности сферы и на внутренней. Какую из них выбрать — это опять вопрос выпуклости/вогнутости, а как следствие, знака радиуса.
Знание z-координаты дает множество возможностей, например, можно воспользоваться z-буфером для проверки видимости.
Для определения цвета пикселя нужно определить текстурные координаты точки X. Нам заданы текстурные координаты вершин треугольника, их нужно интерполировать на точку X. Если мы просто разложим вектор AX по базису векторов AB, AC и нормали, то получим, что в некоторых точках сферического треугольника значение координат в этом базисе будет отрицательным или больше единицы . Это приведет к тому, что визуально сферический треугольник с таким наложением текстуры будет выглядеть "странно", а на стыке треугольников с одинаковыми текстурными координатами будет явно видна граница.
Чтобы избавиться от этих эффектов, я предлагаю разлагать вектор AX по базису векторов AB, AC и OX. Использование вектора OX привносит нелинейные искажения, "растягивающие" текстуру на весь сферический треугольник. Разложение осуществляется следующими формулами (нам нужны только первые две координаты, поэтому третью формулу я опустил):
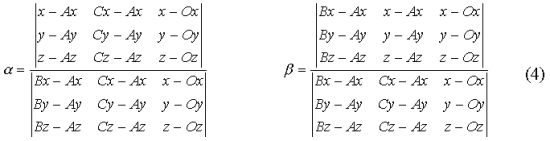
Если ![]() или
или ![]() или
или ![]() , то точка находится за пределами данного сферического треугольника и может быть исключена из дальнейшего рассмотрения.
, то точка находится за пределами данного сферического треугольника и может быть исключена из дальнейшего рассмотрения.
Текстурные координаты (Xu, Xv) находятся по следующим формулам:

Зная текстурные координаты и текстуру, найти цвет пикселя уже легко.
Хотя формулы выглядят довольно громоздко, их программная реализация работает достаточно быстро.
Некоторые проблемы и пути их решения
При моделировании "летающей тарелки" у меня возникла следующая проблема:

Оказалось, что как бы я ни старался, уголки треугольников торчат в месте стыка. Дело в том, что, как я уже писал, сферический треугольник образуется тремя дугами больших кругов. А это значит, что только в районе экватора нижние грани треугольников лежат в одной плоскости. Но тогда "тарелка" вырождается в сферу. Можно разбить каждую половинку на множество сферических треугольников, но это противоречит самой идее использования этих примитивов.
Чтобы избавиться от этих артефактов, я предлагаю следующий метод. Сферическому треугольнику дополнительно назначается плоскость (A, B, C, D), а также два числа Dmin и Dmax — начальное и конечное расстояние от плоскости, диапазон, по которому отсекается треугольник. То есть, в процесс проектирования добавляется проверка:
Подразумевается, что ![]()
Эта проверка позволяет значительно расширить возможности сферических треугольников. Например, используя этот метод, можно получить такой объект:

При этом, падения скорости не наблюдается, временами даже наоборот.
Заключение
Использование сферических треугольников в задачах компьютерной графики имеет как свои плюсы, так и минусы. Очевидно, что эти примитивы не смогут полностью удовлетворить разработчиков трехмерных приложений или вытеснить плоские треугольники. Я ни в коем случае не позиционирую описанные методы как альтернативу существующим системам. Но использование сферических треугольников совместно с другими технологиями способно дать еще одну степень свободы создателям трехмерных миров. Этим, наверное, стоит воспользоваться.


