Теория визуализации информации. Часть 1
Пост опубликован в блогах iXBT.com, его автор не имеет отношения к редакции iXBT.com
Привет, ixbt! Я занимаюсь контентом и подкастами. В одной из передач мы разбираем различные аспекты проектирования и дизайна. В качестве подготовки к одному из последующих выпусков я решил проработать интересный материал на тему визуализации информации. Сегодня я поделюсь переводом первой части авторской статьи.
Мне нравится открывать для себя новые способы мышления. Особенно нравится наблюдать, как смутная идея трансформируется в конкретную концепцию. Ярким примером этого является теория информации. Она дает нам точный язык для описания многих вещей.
Какова степень неопределённости? Как ответить на вопрос B, зная ответ на вопрос A? Чем похож один набор убеждений на другой?
Когда я был ребенком, у меня имелись некоторые нестандартные мысли по этому поводу, но именно теория информации сформировала их в конкретные, мощные идеи, которые имеют множество сфер применения: от сжатия данных до квантовой физики и машинного обучения.
Теория информации выглядит пугающей, но я думаю, что это не так. На самом деле, многие основные идеи можно наглядно объяснить.
Визуализация распределения вероятностей
Прежде чем мы углубимся в теорию информации, давайте подумаем о том, как нам визуализировать простое распределение вероятностей. Нам это понадобится немного позднее, но имеет смысл ответить на этот вопрос сейчас. Кроме того, такие приемы сами по себе довольно полезны.
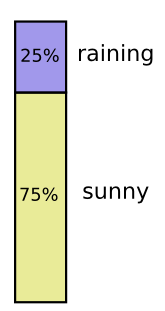
Я живу Калифорнии. Иногда здесь идет дождь, но в основном солнечно. Предположим, что солнечно бывает 75% времени. Это легко изобразить на диаграмме:
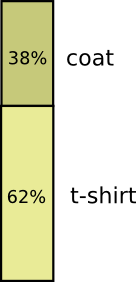
Большую часть времени я ношу футболку, но иногда надеваю пальто. Предположим, что я ношу пальто 38% времени. Изображаем это на диаграмме:
Теперь я хочу объединить обе диаграммы. Это легко, если они никак не взаимодействуют друг с другом, то есть являются независимыми. Например, надену я сегодня футболку или пальто, на самом деле, не зависит от погоды на следующей неделе. Отметим первую переменную по оси X, а вторую – по оси Y:

Обратите внимание на прямые линии: вертикальную и горизонтальную. Так выглядит независимость событий. Вероятность того, что я надел пальто, не влияет на факт выпадения осадков на этой неделе.
Другими словами, вероятность того, что я надену пальто, и на следующей неделе пройдет дождь, есть произведение вероятностей того, что я надену пальто, и что будет дождь. Эти вероятности не влияют друг на друга.
При взаимодействии переменных, для одних пар вероятность увеличивается, а для других уменьшается. Вероятность того, что я надену пальто, когда идет дождь, гораздо выше, потому что переменные коррелируют.
Вероятность того, что я надену пальто в дождливый день выше, чем вероятность того, что я надену пальто в солнечный день.
Визуально это выглядит так: одни области увеличиваются за счет дополнительной вероятности, а другие уменьшаются, потому что эта пара событий маловероятна.
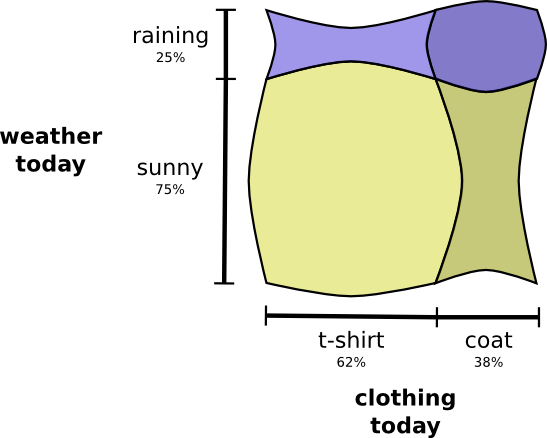
Впечатляет, правда? Но такая схема не очень удобна для понимания.
Давайте сосредоточимся на одной переменной – погоде. Мы знаем вероятность того, каким будет день: солнечным или дождливым. В обоих случаях можно рассмотреть условные вероятности.
Какова вероятность того, что я надену футболку, если на улице солнечно? Какова вероятность того, что надену пальто, если идет дождь?
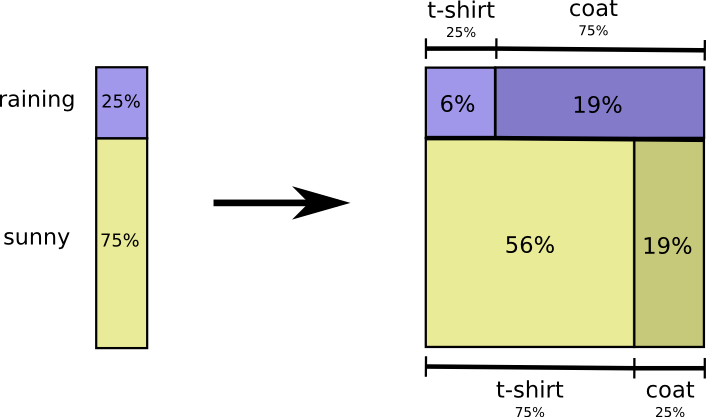
Вероятность того, что пойдет дождь, составляет 25%. Шанс, что я надену пальто в дождливую погоду, равен 75%. Таким образом, вероятность того, что идет дождь, и я в пальто – это 25%, умноженные на 75%, что составляет примерно 19%.
Вероятность того, что идет дождь, и я в пальто, равна вероятности того, что идет дождь, умноженной на вероятность того, что я надену пальто в дождливую погоду.
Это один из возможных случаев фундаментального тождества теории вероятностей. Мы раскладываем функцию на произведение двух множителей. Сначала рассматриваем вероятность того, что одна переменная (погода) примет определенное значение.
Затем рассматриваем вероятность того, что другая переменная (одежда) примет определенное значение, в зависимости от первой переменной.
Для начала произвольно выбираем переменную. Начнем с одежды, а затем рассмотрим погоду, обусловленную одеждой. Это звучит немного странно, поскольку мы понимаем, что, с точки зрения причинно-следственной связи, именно погода влияет на то, что я ношу, а не наоборот… но сейчас это не принципиально.
Рассмотрим пример. Если мы рассматриваем случайный день, то шанс, что я надену пальто, равняется 38%. Какова вероятность того, что пойдет дождь, если я надел пальто? Скорее всего, я надену пальто в дождь, чем в солнечную погоду, но дождь – редкое явление в Калифорнии (поэтому предположим, что вероятность выпадения осадков равна 50%).
Итак, вероятность того, что идет дождь, и я в пальто, равна произведению вероятностей того, что я надену пальто (38%), и что будет дождь, если я в пальто (50%). Это приблизительно 19%.
Это второй способ визуализировать то же распределение вероятностей.
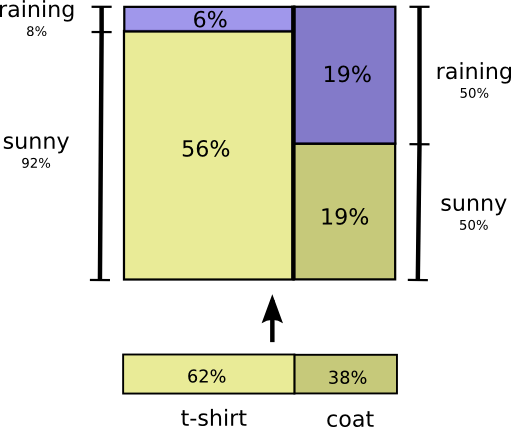
Обратите внимание, что обозначения имеют несколько иной смысл, чем на предыдущей схеме: теперь футболка и пальто – это безусловные вероятности (вероятность носить определенную одежду без учета погодных условий).
Также мы видим, что появились два обозначения вероятностей солнечной и дождливой погоды, в зависимости от того, надел я футболку или пальто. (Возможно, вы слышали о теореме Байеса. Можно использовать её для перехода от одного из этих способов отображения распределения вероятностей к другому).
[Продолжение рассказа опубликовано в блоге университета ИТМО: 1 и 2]











2 комментария
Добавить комментарий
Добавить комментарий