Как упаковать покупки как профессионал: секреты теории упаковки

Вы когда-нибудь задумывались, как правильно упаковать продукты в сумку или корзину, чтобы они не помялись, не разбились и не заняли слишком много места? Возможно, вы даже применяли какие-то эмпирические правила, например, класть тяжелые и крупные предметы на дно, а легкие и мелкие — сверху. Но знаете ли вы, что за этим простым действием стоит целая наука, которая называется теория упаковки?

Теория упаковки — это раздел математики, который изучает способы размещения объектов различной формы и размера в контейнеры с минимальным количеством пустого пространства. Эта задача имеет множество практических применений в разных областях, таких как логистика, складирование, транспортировка, производство и даже астрономия. Например, как упаковать груз в грузовик или контейнер так, чтобы использовать всю доступную площадь и объем? Как уложить яйца в коробку так, чтобы они не треснули? Как расставить спутники на орбите так, чтобы они не столкнулись друг с другом?

Оказывается, что эти задачи не так просты, как кажутся на первый взгляд. Даже для самых простых геометрических фигур, таких как круги и квадраты, не существует общих формул или алгоритмов, которые бы давали оптимальное решение для любого случая. В некоторых случаях оптимальное решение известно или доказано математически, но в большинстве случаев оно либо неизвестно, либо является предметом спора или гипотез. Поэтому часто приходится прибегать к приближенным методам или компьютерным симуляциям.

Давайте рассмотрим несколько примеров задач упаковки и попробуем найти оптимальные или приближенные решения для них.

Упаковка кругов

Представьте, что вы хотите купить апельсины в магазине и уложить их в круглую корзину. Какое максимальное количество апельсинов вы сможете упаковать в корзину? Эта задача эквивалентна задаче упаковки одинаковых кругов в большой круг. Оказывается, что оптимальный способ упаковки зависит от соотношения радиусов маленького и большого круга. Если радиус большого круга больше чем в 2.1547 раза радиус маленького круга, то оптимальное решение состоит в том, чтобы уложить маленькие круги в шестиугольную решетку (как пчелы строят свои соты). Если же радиус большого круга меньше или равен этому числу, то оптимальное решение может отличаться от шестиугольной решетки и зависит от конкретного значения радиуса. Например, если радиус большого круга равен двум радиусам маленького круга, то оптимальное решение состоит в том, чтобы уложить четыре маленьких круга в углах квадрата, вписанного в большой круг.

Упаковка квадратов

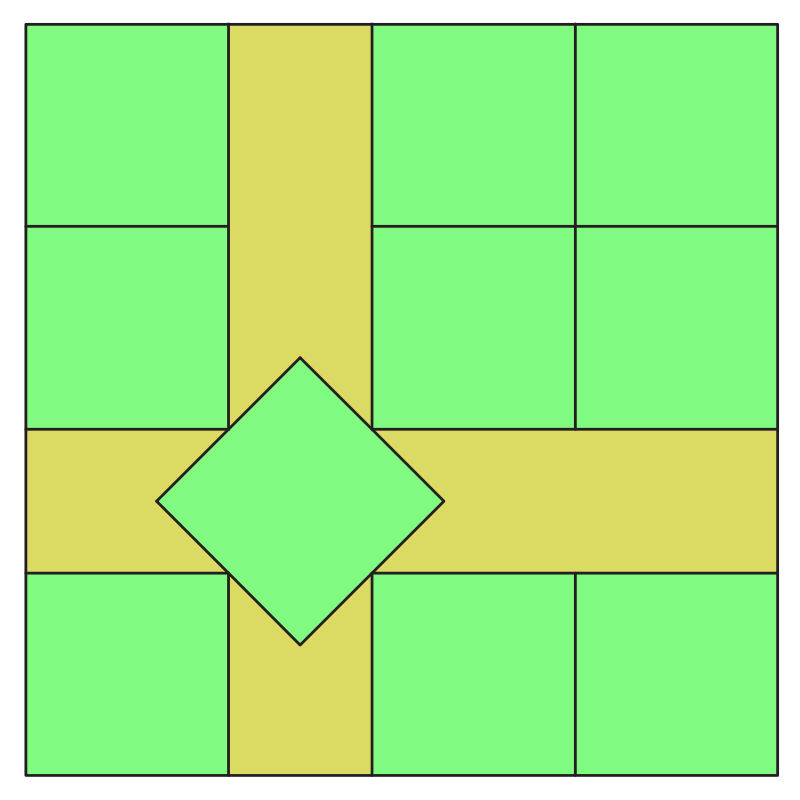
Теперь представьте, что вы хотите купить сыр в магазине и уложить его в квадратную коробку. Какое максимальное количество сыра вы сможете упаковать в коробку? Эта задача эквивалентна задаче упаковки одинаковых квадратов в большой квадрат. В отличие от задачи упаковки кругов, для этой задачи существует простое и элегантное решение: нужно уложить маленькие квадраты в ряды и столбцы, параллельные сторонам большого квадрата. Таким образом, можно упаковать максимальное количество квадратов, равное квадрату целой части от деления стороны большого квадрата на сторону маленького квадрата. Например, если сторона большого квадрата равна 10 см, а сторона маленького квадрата равна 3 см, то можно упаковать 9 маленьких квадратов (3 на 3).

Упаковка прямоугольников

А что если вы хотите купить шоколадные батончики в магазине и уложить их в прямоугольную коробку? Какое максимальное количество батончиков вы сможете упаковать в коробку? Эта задача эквивалентна задаче упаковки одинаковых прямоугольников в большой прямоугольник. Эта задача уже намного сложнее предыдущих, так как теперь нужно учитывать не только размеры, но и ориентацию прямоугольников. В общем случае оптимальное решение для этой задачи неизвестно и может зависеть от соотношения сторон маленького и большого прямоугольника. Однако, для некоторых специальных случаев оптимальное решение известно или доказано. Например, если стороны маленького прямоугольника являются делителями сторон большого прямоугольника, то оптимальное решение состоит в том, чтобы уложить маленькие прямоугольники в ряды и столбцы, параллельные сторонам большого прямоугольника. Если же стороны маленького прямоугольника не являются делителями сторон большого прямоугольника, но являются делителями диагонали большого прямоугольника, то оптимальное решение состоит в том, чтобы уложить маленькие прямоугольники по диагонали большого прямоугольника. В остальных случаях оптимальное решение может быть найдено только путем перебора или приближенных методов.

Как видим, задачи упаковки имеют разную степень сложности в зависимости от формы и размера объектов и контейнеров. Некоторые из них имеют простые и элегантные решения, а некоторые до сих пор остаются загадкой для математиков. Но почему эти задачи так важны и интересны? Во-первых, они имеют множество практических применений в разных областях, где важно экономить пространство, время и ресурсы. Во-вторых, они позволяют изучать свойства и связи между различными геометрическими фигурами и их комбинациями. В-третьих, они порождают множество интересных фактов.

Вот некоторые из этих фактов:

• Существует бесконечное количество способов упаковать одинаковые круги в плоскость, но только шесть способов упаковать одинаковые квадраты в плоскость.
• Самый плотный способ упаковки одинаковых кругов в плоскость достигается при шестиугольной решетке, при которой каждый круг касается шести других кругов. Этот способ упаковки называется гексагональным или регулярным. При этом плотность упаковки равна примерно 0.9069, то есть 90.69% площади плоскости занято кругами, а 9.31% - пустотами.
• Существует еще один способ упаковки одинаковых кругов в плоскость, при котором каждый круг также касается шести других кругов, но решетка не является шестиугольной, а состоит из чередующихся рядов трех- и четырехугольников. Этот способ упаковки называется Аполлониевым или иррегулярным. При этом плотность упаковки также равна примерно 0.9069, то есть такая же, как у гексагональной решетки. Это явление называется изоденсностью.

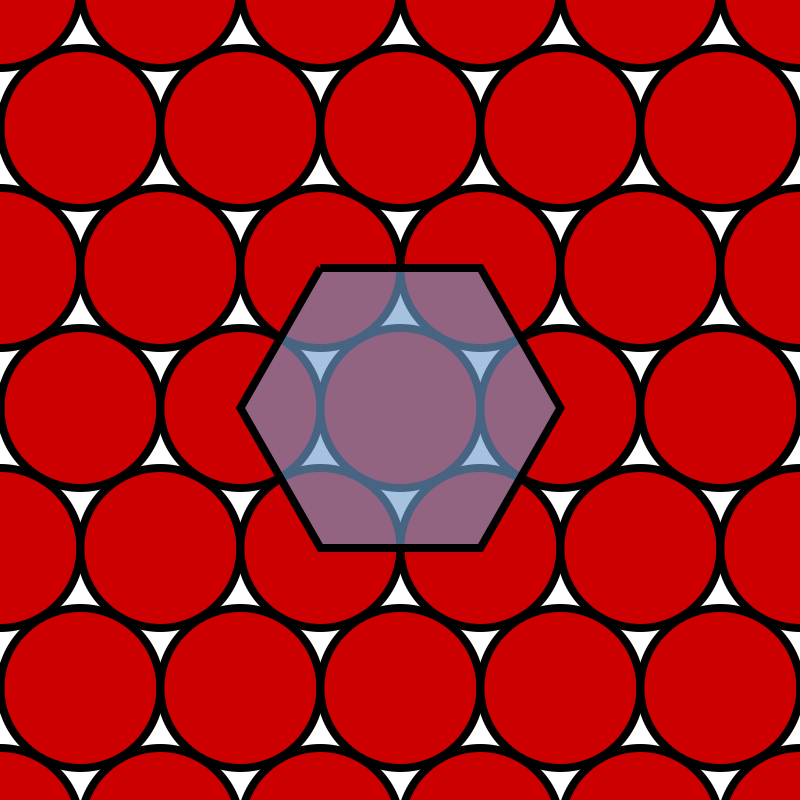
Гексагональная и Аполлониева решетки являются единственными способами упаковать одинаковые круги в плоскость с максимальной плотностью. Эта гипотеза называется гипотезой Кеплера или гипотезой о плотнейшей упаковке кругов. Она была сформулирована в 1611 году немецким астрономом и математиком Иоганном Кеплером, но доказана только в 1998 году американским математиком Томасом Хейлсом с помощью компьютерной проверки более 5000 случаев.

• Существует бесконечное количество способов упаковать одинаковые квадраты в плоскость, но только два способа упаковать одинаковые квадраты в плоскость с максимальной плотностью. Один из них — это упаковка в ряды и столбцы, параллельные сторонам плоскости, при которой плотность упаковки равна 1, то есть 100% площади плоскости занято квадратами. Другой — это упаковка в ряды и столбцы, составляющие угол 45 градусов с сторонами плоскости, при которой плотность упаковки также равна 1, но требуется больше квадратов для заполнения той же площади.
• Существует бесконечное количество способов упаковать одинаковые треугольники в плоскость, но только три способа упаковать одинаковые треугольники в плоскость с максимальной плотностью. Один из них — это упаковка в шестиугольную решетку, состоящую из равносторонних треугольников, при которой плотность упаковки равна примерно 0.9069, то есть такая же, как у гексагональной решетки кругов. Другой — это упаковка в квадратную решетку, состоящую из прямоугольных треугольников с углами 45, 45 и 90 градусов, при которой плотность упаковки равна 1, то есть такая же, как у решетки квадратов. Третий — это упаковка в шестиугольную решетку, состоящую из прямоугольных треугольников с углами 30, 60 и 90 градусов, при которой плотность упаковки также равна 1.
• Существует бесконечное количество способов упаковать разные фигуры в плоскость, но не все из них имеют максимальную плотность. Например, если вы хотите упаковать звезды в плоскость, то вы не сможете достичь плотности больше примерно 0.7476. Если же вы хотите упаковать сердца в плоскость, то вы не сможете достичь плотности больше примерно 0.7042. А если вы хотите упаковать полумесяцы в плоскость, то вы не сможете достичь плотности больше примерно 0.6617.

Как мы видим, задачи упаковки не только полезны и сложны, но и красивы и занимательны. Они показывают, как математика может помочь нам эффективнее упаковывать покупки, но и открывать новые горизонты для исследования и творчества.