Почему прорыв в обучении часто начинается с провала? Ученые создали единую модель мастерства – как она работает?

Вы когда-нибудь бились над новым навыком? Может, пытались выучить язык, освоить гитару или даже жонглировать тремя апельсинами? Сначала — энтузиазм, часы практики до изнеможения. Потом — спад мотивации, скука, желание всё бросить. А иногда, спустя недели или месяцы, вдруг — прорыв! То, что казалось невозможным, получается легко и естественно.

Обучение — это странный зверь. Оно происходит на совершенно разных скоростях. Вот вы на минуту сосредоточились, пытаясь понять сложную концепцию. А вот вы годами оттачиваете мастерство, как Пикассо у холста или гроссмейстер за шахматной доской. Как эти мимолётные мгновения усилий и усталости складываются в долгий путь к вершинам мастерства? Почему иногда мы застреваем на плато, а иногда вдруг делаем гигантский скачок вперед?

Долгое время учёные рассматривали эти процессы как бы по отдельности. Одни изучали кривые обучения, показывающие медленный прогресс за месяцы и годы. Другие — сиюминутные колебания мотивации и усталости. Но как связать одно с другим? Как понять целостную картину?

Математика против хаоса: Можно ли описать обучение формулами?

Представьте себе, что можно создать своего рода «симулятор обучения» — математическую модель, которая учитывала бы и долгий марафон к мастерству, и короткие спринты ежедневных усилий. Именно такую амбициозную задачу поставили перед собой исследователи Минчжэнь Лу, Тайлер Маргетис и Вики Чуцяо Ян.

Они решили отойти от простых описаний и создать модель, основанную на «первых принципах» — то есть, включить в неё только самые необходимые компоненты, чтобы посмотреть, смогут ли они объяснить сложные и разнообразные закономерности обучения, наблюдаемые в реальной жизни, от жонглирования до игры в шахматы.

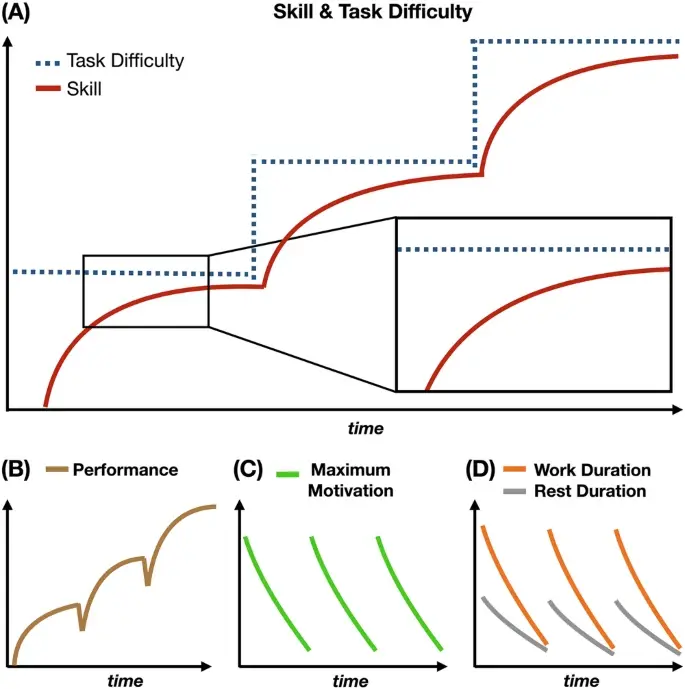
Что же это за компоненты? Учёные выделили два уровня переменных.

На длинной дистанции:

1. Уровень Навыка (S): Насколько хорошо вы что-то умеете.
2. Сложность Задачи (T): Насколько трудна задача, которую вы пытаетесь решить.
3. Эффективность Исполнения (E): Насколько хорошо вы применяете свой навык прямо сейчас (ведь можно быть мастером, но от усталости делать ошибки). Ваша реальная производительность — это сочетание навыка и эффективности (S умножить на E).

На короткой дистанции (прямо сейчас):

1. Мотивация (M): Ваше желание работать над задачей.
2. Усталость (F): Накопленное утомление.
3. Решение «Работать или Отдыхать» (p): Простое да/нет, зависящее от баланса мотивации и усталости.

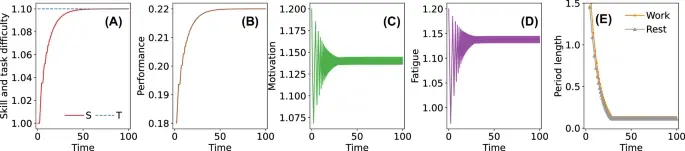
И вот тут начинается самое интересное — эти уровни постоянно взаимодействуют!

Внутренний «переключатель»: Работаем или отдыхаем?

Как модель решает, пора ли браться за дело или сделать перерыв? Очень просто и жизненно: если мотивация (M) превышает усталость (F) плюс некий небольшой «порог усилия» (ведь начать всегда чуть сложнее), то вы работаете (p=1). Как только усталость догоняет или перегоняет мотивацию (M ≤ F), вы останавливаетесь (p=0).

Во время работы усталость накапливается (причём довольно быстро, линейно). Во время отдыха — спадает (постепенно, по экспоненте, как мы и чувствуем — сначала отдых очень эффективен, потом медленнее).

А мотивация? Она тоже не стоит на месте. Она стремится вернуться к некоему базовому уровню, но при этом подпитывается успехами! Если вы чувствуете, что учитесь чему-то новому (навык S растет) или успешно применяете то, что уже умеете (исполнение E высокое), ваша мотивация получает дополнительный импульс. Знакомо, правда? Успех порождает желание продолжать!

«Сладкое пятно» обучения: Почему слишком легко и слишком сложно — плохо?

Модель показывает кое-что любопытное о росте самого навыка (S). Оказывается, навык растет быстрее всего, когда сложность задачи (T) чуть-чуть выше вашего текущего уровня (S). Слишком легкая задача (T ниже S) — скучно, роста почти нет. Непосильная задача (T намного выше S) — фрустрация, вы бьетесь головой о стену, и рост тоже минимален. Это та самая «зона ближайшего развития», о которой говорят педагоги — вызов должен быть посильным, но все же вызовом.

А вот эффективность исполнения (E) — наоборот. Лучше всего мы действуем, когда задача чуть проще или равна нашему навыку (T ≤ S). Как только задача становится сложнее, наша эффективность падает — мы начинаем делать ошибки, действуем медленнее.

Именно этот баланс между оптимальной сложностью для обучения и оптимальной сложностью для исполнения объясняет многие странности нашего прогресса.

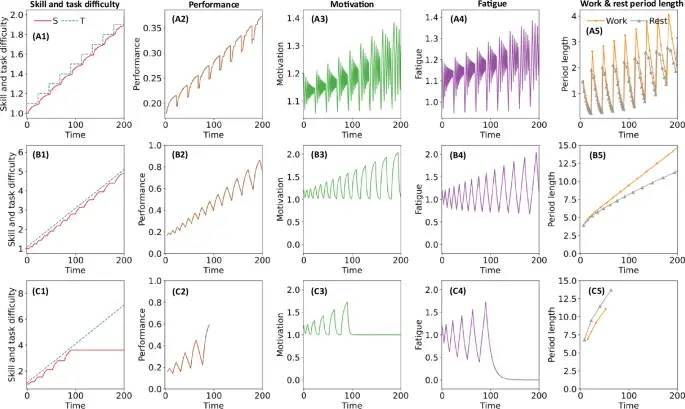
От плато к прорывам: Как модель объясняет кривые обучения?

Теперь посмотрим, как эти внутренние механизмы создают знакомые нам картины обучения:

1. Плато (Задача не меняется): Вы решаете одну и ту же задачу (T постоянно). Сначала навык (S) быстро растет. Мотивация высокая, вы работаете долго. Но по мере приближения S к T, задача становится слишком легкой. Темп обучения падает. Мотивация снижается. Вы работаете короче, отдыхаете чаще. Наступает плато — навык и производительность перестают расти. Знакомо?
2. Лестница (Сложность растет скачками): Представьте, вы освоили один уровень игры и перешли на следующий (T резко увеличилось). Что предсказывает модель? Сначала — падение производительности! Новая задача сложнее, ваша эффективность (E) падает. Но! Если новый уровень сложности попал в «сладкое пятно» (чуть выше вашего S), ваш навык (S) снова начинает быстро расти. Мотивация подскакивает! Вы снова готовы работать усердно. Освоив этот уровень, вы снова выходите на плато… до следующего скачка сложности. Модель идеально воспроизводит эти «плато-падение-взлет», которые часто видят психологи в реальных экспериментах!
3. Непрерывный Рост (Сложность плавно увеличивается): А что если сложность растет постоянно, как при беге на все более длинные дистанции? Если темп роста сложности умеренный, модель показывает устойчивый рост навыка и производительности. Более того, пиковая мотивация и продолжительность рабочих сессий тоже могут расти! Вы как бы постоянно находитесь в потоке, где вызов соответствует вашим возможностям. Но горе тому, кто повышает планку слишком быстро! Модель показывает, что в этом случае навык не успевает подтягиваться, мотивация падает до нуля, и человек просто «сходит с дистанции».

Вы «ученик» или «исполнитель»? Ваш внутренний компас

Модель учитывает и индивидуальные различия. Помните, мотивация подпитывается и ростом навыка, и успешным исполнением? А что, если у разных людей разный баланс?

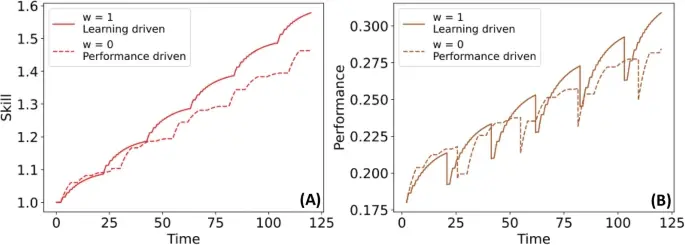
Учёные ввели параметр 'w', который отражает, что для вас важнее: сам процесс обучения (w близко к 1) или демонстрация уже имеющегося мастерства (w близко к 0).

• «Ученики» (высокое w): Они больше мотивированы ростом навыка. Модель показывает, что такие люди смелее берутся за сложные задачи, даже если это временно снижает их производительность (те самые «падения» на лестнице обучения). Они чаще испытывают трудности в моменте, но в долгосрочной перспективе их навык растет быстрее и достигает больших высот!
• «Исполнители» (низкое w): Их больше мотивирует безупречное выполнение. Они предпочитают задачи, с которыми точно справятся. Их кривая обучения более гладкая, без резких падений. Но, избегая сложных вызовов, они в итоге медленнее прогрессируют и могут не достичь того же уровня мастерства, что и «ученики».

Узнаете себя? Этот простой параметр в модели может объяснить, почему одни люди постоянно ищут новые вызовы, а другие предпочитают оттачивать то, что уже умеют.

Математика потока и ограничения модели

Интересно, что когда модель симулирует условия оптимального вызова (задача не слишком простая и не слишком сложная), она воспроизводит картину, очень похожую на знаменитое «состояние потока»: высокая мотивация, способность долго работать, несмотря на накапливающуюся усталость. Возможно, математикам удалось нащупать глубинные механизмы этого неуловимого состояния?

Конечно, эта модель — не истина в последней инстанции. Она универсальна и не учитывает специфику конкретных задач (учить стихи — не то же самое, что учиться плавать). Она не включает внешние факторы: поддержку тренера, дедлайны, влияние других дел или даже просто необходимость спать по ночам. Она рассматривает один навык, а в жизни мы часто осваиваем несколько параллельно.

Но её ценность не в абсолютной точности, а в том, что она предлагает единый каркас для понимания обучения на всех его уровнях. Она показывает, как сложные, долгосрочные процессы могут вырастать из простых, краткосрочных взаимодействий мотивации, усталости и усилий. Она связывает воедино разные области психологии и педагогики.

Так что в следующий раз, когда вы будете радоваться прорыву или расстраиваться из-за застоя в обучении, помните: под капотом вашего сознания идут сложные, динамичные процессы. И, возможно, теперь вы чуть лучше понимаете их загадочную логику. Путь к мастерству — это не прямая линия, а увлекательный танец между вызовом, усилием и отдыхом, который теперь можно описать даже языком математики.