Как потерпел крах последний аргумент эйнштейновского реализма против квантовых случайностей?
Квантовая механика — область, мягко говоря, контринтуитивная. Здесь привычные вопросы выворачиваются наизнанку, а попытки найти хоть какой-то здравый смысл порой кажутся безнадежными. Тем не менее, стремление понять фундаментальные принципы мироздания не дает покоя. И казалось, что такой способ был. Но только до тех пор, пока Джон Белл не вывел свои легендарные неравенства. Давайте обо всём по порядку.
Проблематика ситуации
Уже ни для кого не секрет, что до момента измерения квантовая частица ведёт себя одним образом, а после — другим. Что-то происходит на границе этого процесса или как простое детектирование может что-то поменять? Так звучит парадокс наблюдателя и к этому есть несколько подходов. Один из них хорошо сочетается с нашей интуицией.
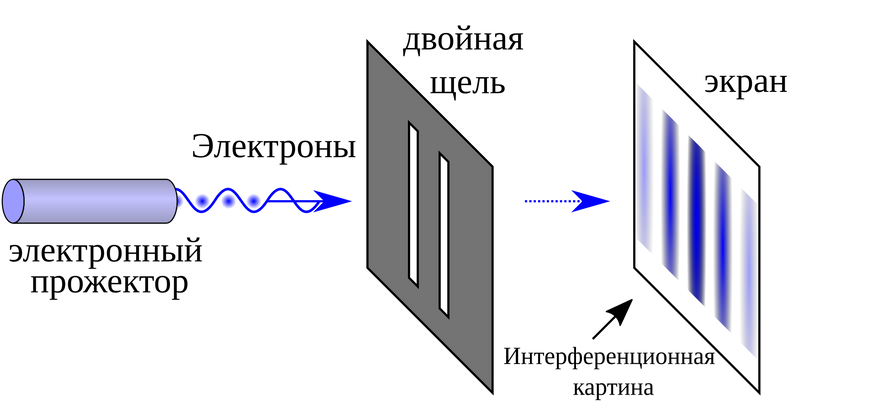
Итак, что представляет собой выбор квантового состояния? Является ли это созданием из ничего, где до измерения не существовало никакого предопределенного исхода? Или же это лишь процесс выявления одного из уже существующих, но скрытых от нас состояний, заложенных в структуру системы?
Представим простую аналогию. Есть три уникальных тропы, ведущих к вершине горы, а других путей не существует. Исключим полностью возможность создания новых троп, комбинируя участки существующих — это невозможно в силу каких-либо гипотетических ограничений. Варианта всего три и точка.
Теперь представим, что мы проводим «измерение», цель которого установить, какой тропой путник достиг вершины. Согласно моему пониманию проблемы, в квантовом мире измерение должно выявить один из этих трех существующих маршрутов, выбирая его абсолютно случайным образом.
Однако, сторонники радикальной интерпретации квантовой механики утверждают, что до момента измерения не существует вообще никаких троп. Сама тропа возникает только в момент взаимодействия наблюдателя с системой или с её поиском на карте. Эта тропа не совпадает ни с одной из известных нам заранее. Ни один из трех существовавших ранее вариантов не является истинно случайным результатом в квантовом смысле. Настоящая квантовая случайность предполагает создание чего-то совершенно нового «на лету».
Но это же нонсенс. В любой физической системе сложно представить ситуацию, где выбор не происходил бы из некоторого множества предопределенных возможностей. Так или иначе, любой вариант уже имеет математическое его описание.
В ответ я обычно слышу обвинение в приверженности теории скрытых параметров. Безнадежно устаревшей концепции, утверждающей, что под покровом случайности скрываются детерминированные причины. Физики сегодня полагают, что случайность абсолютно фундаментальна и что это не математический артефакт, а квинтэссенция самой реальности.
Что такое скрытые параметры?
Концепция скрытых параметров предполагает наличие у объектов свойств, которые остаются невидимыми для нас, недоступными для прямых измерений, но при этом оказывают влияние на наблюдаемые нами явления. В сфере квантовой механики, эта идея воплощается в гипотезе о существовании у систем (например, элементарных частиц) внутренних, экспериментально неотслеживаемых характеристик, которые, тем не менее, однозначно определяют результаты любых проводимых измерений.
Оглядываясь на историю науки, можно вспомнить множество событий, которые в прошлом воспринимались как нечто непостижимое, приписывались чистой случайности или даже потусторонним силам. Даже огонь когда-то был окутан мистическим ореолом. Но, по мере углубления исследований, выяснялось, что за кажущимся хаосом всегда скрывается определенный фактор (или несколько факторов), оказывающий влияние на ход событий. Просто на тот момент этот фактор оставался за пределами возможностей для обнаружения и изучения, в силу ограниченности имевшихся научных инструментов и знаний.

Когда квантовая теория только формировалась, появилось представление о парадоксе ЭПР (парадокс Эйнштейна, Подольского и Розена или квантовая запутанность). Эйнштейн на тот момент высказался, что квантовая природа противоречит здравому смыслу и что по всей видимости парадокс есть непонимание некоторых важных факторов, которые оказывают влияние на систему, но недоступны физикам того времени. Эти факторы и получили название скрытых параметров. Подход тогда именовался локальным реализмом.
В данном контексте, под реализмом подразумевается, что физические свойства объектов, будь то спин, поляризация или что-либо еще, имеют конкретные, определенные значения, независимо от того, производим мы измерение или нет. Иными словами, у частицы существует некое предопределенное значение спина, даже если мы еще не попытались его зафиксировать.
Принцип локальности, в свою очередь, утверждает, что на объект может оказывать влияние исключительно его ближайшее окружение, и ничто не может передаваться быстрее скорости света. Это влечет за собой следствие, что измерение спина одной частицы в паре, находящейся в состоянии квантовой запутанности, не может мгновенно повлиять на спин другой частицы, удаленной на значительное расстояние.
На первый взгляд, эти представления кажутся абсолютно логичными и интуитивно понятными. Но почему же эта, казалось бы, безупречная логика, вызвала столь ожесточенную критику и привела к пересмотру фундаментальных основ физики?
Неравенства Белла и крах реализма
В самом разгаре дебатов между реализмом и абсолютной квантовой индетерминированностью, Джон Белл представил серию математических неравенств, которые должны соблюдаться при условии верности принципа локального реализма. Эти неравенства устанавливают строгую зависимость между результатами измерений различных характеристик квантово-запутанных частиц (например, спина). Нарушение этих неравенств служит аргументом в пользу квантовой случайности как доминирующего принципа.
Неравенства Белла, по существу, представляют собой математическое выражение проблемы, связанной с концепцией скрытых параметров. Без углубления в сложные математические детали, суть можно объяснить следующим образом.
Создается некая математическая модель, в которой сравниваются выводы, полученные для системы со скрытыми параметрами и для системы без них. Если введение в уравнения коэффициентов, отражающих потенциальное наличие скрытых параметров, не оказывает влияния на поведение системы, то делается заключение об их отсутствии.
Анализ показал, что присутствие скрытых параметров не меняет математическую структуру системы, что, казалось бы, должно исключать возможность существования каких-либо «заранее заданных» значений или реальных факторов, влияющих на результат измерения.
Однако, тут есть два существенных «но».
Первое: неравенства Белла не доказывают полное отсутствие всех видов скрытых параметров. Их вывод однозначен лишь в отношении локальных скрытых параметров, то есть тех, которые не могут передавать информацию мгновенно на большие расстояния. И именно невозможность объяснить все предсказания квантовой механики таким способом и была доказана. Это принципиально важный нюанс.
Второе: теория локальных скрытых параметров предполагает, что именно эти скрытые переменные детерминируют результат измерения. Но эксперименты неоднократно демонстрировали нарушение неравенств Белла, что делает эту теорию неспособной объяснить квантовую реальность. При этом, сами рассуждения носят сугубо математический характер. По сути, мы пытаемся доказать отсутствие скрытых причин, используя для этого математический аппарат, который изначально считался неполным для описания квантовых явлений. Это вызывает вопросы и подчеркивает доминирование математического подхода над физическим осмыслением.
Между тем, работу неравенств Белла в итоге подтвердили экспериментально. Работ на этот счёт довольно много и результаты всегда одинаковые. Один из «свежих экспериментов» проведен в 2023 году. Он описан в статье «Loophole-free Bell inequality violation with superconducting circuits» и опубликован в журнале Nature 10 мая 2023 года.
Вероятно, нам всё-таки придётся отказаться от попыток найти какой-то эйнштейновский реализм в осознании квантовой случайности.
Источник: ru.freepik.com











1 комментарий
Добавить комментарий
Добавить комментарий