DX Current
Настоящее аппаратного ускорения графики

Журнал iXBT.com за весь 2007 год Узнайте о чём мы писали

Замечательным аспектом данного труда является полное отсутствие какого либо предисловия и заключения. Что, возможно, символизирует собой непрерывность технического прогресса в данной области. Или ничего не символизирует.

Три заповеди

Основное влияние на архитектуру современных аппаратных графических решений оказывают три факта:

1. Высокая параллельность графических алгоритмов.
2. Потоковый характер построения изображения (графического конвейера).
3. Ориентация графических алгоритмов на вычисления, а не на принятие решений.

Несмотря на то, что эти сентенции звучат как банальные истины, предлагается немного помедитировать над ними - именно в них сокрыто понимание современных графических архитектур и их развития. Итак:

Пространная медитация над ними

Большинство первичных данных, с которыми оперирует современная компьютерная графика (вершины, векторы, значения цвета) являются векторами. Причем, замечательным фактом является то, что размерность этих данных практически никогда не превышает 4. Другим замечательным фактом является то, что по статистике, большинство операций, выполняемых ускорителем, будут векторными, причем, как правило, 3- и 4-мерными. Вот почему современные ускорители состоят практически исключительно из четырехмерных векторных ALU, исполняющих одну операцию над 4 компонентами того или иного формата. Небольшой ликбез - как это выглядит на практике:

Нам надо сложить два цвета. Каждый из них вектор из четырех компонент - R, G, B, А - красной, зеленой, синей и опционального альфа коэффицента - степени прозрачности.

	R	G	B	A
Цвет1	0	255	0	0
Цвет2	100	0	100	0
Операция +	+	+	+	+
Результат	100	255	100	0

Очевидно, что т.к. во время этих вычислений данные никак не зависят друг от друга, мы можем выполнить их параллельно, т.е. за один шаг. Для этого нам не надо иметь 4 полноценных ALU, а можно ограничится одним векторным ALU (т.н. SIMD - одна инструкция - много данных), которое имеет общую контрольную логику и может выполнять одну операцию над четырьмя исходными наборами данных. Однако реально все несколько сложнее. Во-первых могут быть случаи, когда данные начинают взаимодействовать друг с другом. Например, по той или иной причине мы хотим:

Результат.R = Цвет1.R + Цвет2.G

Рассчитать красный цвет результата как сумму зеленой и красной компоненты исходных данных. Для этого нам необходимо реализовать в нашем ALU механизм произвольной коммутации компонент векторов, перед тем как они будут обработаны:

	R	G	B	A
Цвет1	0	255	0	0
Цвет2	100	0	100	0
Коммутация 1	Цвет1.R (0)	Цвет1.G	Цвет1.B	Цвет1.A
Коммутация 2	Цвет2.G (0)	Цвет2.G	Цвет2.B	Цвет2.A
Операция +	+	+	+	+
Результат	0	255	100	0

Таким образом, мы экономим время на пересылках данных, хотя можно сделать и отдельную операцию для перестановки компонент векторов, а не оснащать такой функциональностью ALU, с точки зрения производительности приведенный подход более рационален.

Однако продолжим медитировать - это еще только начало. В реальных графических алгоритмах нас может не устроить тот факт, что операция над всеми компонентами одна и таже. Например, компонента A зачастую обрабатывается по иным правилам:

	R	G	B	A
Цвет1	0	255	0	255
Цвет2	100	0	100	0
Операция +	+	+	+	*
Результат	100	255	100	0

Здесь мы должны решать: либо разбивать эту операцию на две последовательные, либо научить наше ALU делать операции по схеме 3+1 (RGB+A) - т.е. фактически иметь два ALU, одно трехкомпонентное и одно двухкомпонентное. Да, сложность выше, но и производительность зачастую тоже - фактически две операции выполняются параллельно, за время одной.

Следующий шаг на этом пути - позволить двум операциям выполняться над произвольными компонентами, не только по схеме 3+1 но и по схеме 2+2:

	R	G	B	A
Цвет1	0	255	0	255
Цвет2	100	0	100	0
Операция +	+	+	*	*
Результат	100	255	0	0

Ведь в реальных задачах мы будем сталкиваться и с ситуациями, когда нам надо обработать только двумерные векторы или скалярные величины (особенно это касается пиксельных конвейеров чипа и пиксельных алгоритмов) и тогда мы сможем оптимизировать вычисления, выполняя две операции одновременно. Будет приятно, если даже в этом случае половина транзисторов ALU не будет простаивать, а займется делом, пусть и другим.

Итак, современные графические ALU - векторные, до 4 компонент, с произвольной перестановкой компонент перед вычислениями, с возможностью выполнять разные операции по схеме 3+1 или даже менее часто востребованной, но все равно потенциально выгодной 2+2.

Но, параллельность на уровне компонент векторов это только первый уровень. Мы ограничены лишь 4 компонентами. Основная же прелесть графических алгоритмов в том, что отдельные объекты, обрабатываемые в графическом конвейере, как правило, не зависят друг от друга. Возьмем, например, вершины треугольника. Все три вершины будут обработаны по одному и тому же алгоритму, и более того, совершенно не важен порядок их обработки - во время вычислений операции со второй вершиной мы никогда не интересуемся результатами или ходом обработки первой. Поэтому ничего не мешает нам обрабатывать сразу несколько вершин параллельно. Вот почему в современных графических ускорителях может быть 3 или 4 вершинных процессора. С пикселями дело обстоит еще оптимистичнее - как известно пикселей нам надо закрасить гораздо больше чем, например, трансформировать вершин, и современные ускорители обрабатывают 4 или 8 пикселей одновременно, а грядущие, несомненно, будут еще больше.

Здесь есть один очень важный момент. Если алгоритм обработки не предусматривает проверки каких-либо условий во время исполнения, и действия над всеми вершинами или пикселями будут всегда выполняться одинаковые то все просто:

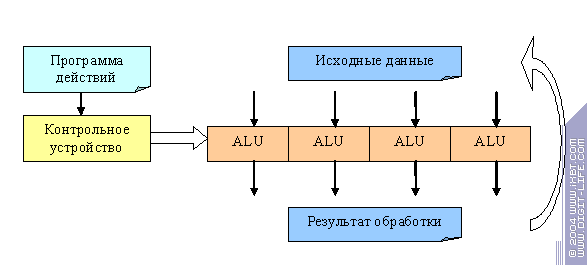
У нас есть одно контрольное устройство, которое в соответствии с программой действий настраивает набор из ALU на какие-либо операции и несколько параллельно обрабатываемых объектов, скажем вершин или пикселей. Устройство, согласно программе действий, конфигурирует ALU на выполнение некой команды, все данные параллельно за один шаг проходят через эту команду, затем устройство конфигурирует следующую команду, данные заново поступают на вход и т.д. пока программа действий себя не исчерпает (в современных ускорителях такие программы могут быть достаточно разнообразными и длинными, они и называются шейдерами, пиксельными или вершинными в зависимости от того с какими объектами работают).

Самое приятное в этой картине то, что данных и ALU может быть сколько угодно (в разумных пределах разумеется), и поэтому мы можем спокойно растить мощь ускорителя простым клонированием ALU. Причем, контрольное устройство остается у нас одно, что сильно экономит транзисторы. Однако, в новых стандартах шейдеров DirectX (пиксельные и вершинные шейдеры 3.0) появились условия. Обработка может быть различной не только в зависимости от констант (что фактически лишь иллюзия выбора - ведь все вершины или пикселы обрабатываются одинаково), а и в зависимости от того, какие исходные данные у нас есть. Это значит что мы не можем больше разделять одно контрольное устройство на все ALU, и нам необходимо сделать действительно полноценные параллельные процессоры, которые хотя и будут руководствоваться общей программой действий, но смогут исполнять ее асинхронно, по-разному.

Здесь начинаются всякие неприятности, например, вопросы синхронизации. Одна вершина или пиксель может быть обработана за меньшее число операций, чем другая. Что делать дальше? Ждать окончания обработки всех объектов, чтобы начать обрабатывать новую порцию или запускать новые объекты по мере освобождения процессоров? Второй подход использует ресурсы железа оптимально, но требует более сложной контрольной логики а, следовательно, еще больше транзисторов.

Возможно и компромиссное решение. У нас по-прежнему есть только одно контрольное устройство, и каждый обрабатываемый объект проходит одинаковый набор операций, но в зависимости от того - выполнено ли некое условие, результаты этих операций либо принимаются, либо откидываются и не изменяют состояние объекта. Т.е. мы выполняем все возможные ветки условия, и «да» и «нет», половину действий проводя в холостую. Но, мы не теряем синхронизации, обрабатывая все одновременно под управлением одного контрольного устройства:

Шаги:	Объект 1	Объект 2	Объект 3	Объект 4
Проверка условия	Да	Нет	Да	Нет
Если да +	+	Простаиваем	+	Простаиваем
Если нет +	Простаиваем	-	Простаиваем	-
Если да *	*	Простаиваем	*	Простаиваем
+	+	+	+	+

Насколько выгоден подобный подход зависит от того, насколько велика доля условных операций. В нашем примере из 20 операций - 6 были холостыми. В будущем, по мере увеличения гибкости программ обработки графических данных, выгода будет сходить на нет, и предпочтение будет отдано полностью независимым процессорам, однако в данный момент подобный компромисс выглядит вполне оправданным.

Но, по мере погружения в глубины медитации мы понимаем, что и параллельность на уровне объектов (тех же пикселей и вершин) не является последним шагом к увеличению производительности! Мы можем ввести достаточно парадоксальное понятие параллельности, во времени : продемонстрировав что, существуют случаи, когда замена шила на мыло может принести немалую выгоду.

Как выглядит типичная последовательность действий при закраске пикселов:

• Выборка значения текстуры 1.
• ...
• Выборка значения текстуры N.
• Вычисления.
• Запись результатов.

Сама по себе операция выборки текстур (а также фильтрации, подготовки текстурных координат, расчета MIP уровня и множества других действий, скрывающихся за понятием «выборка тут») может требовать более сотни ступеней и соответственно, при пошаговом исполнении длиться более ста тактов. Разумеется, нас не устраивает такой оборот дела, но именно тот факт, что обрабатываемые параллельно, да и те, что будут обрабатываться потом, в следующие заходы, пикселы не зависят друг от друга, позволяет нам создать огромной длины, более чем с сотней стадий, конвейер, занимающийся только выборкой текстур и выдающий, в случае если все идет хорошо, по результату за такт, как и положено. В центральных процессорах ~20 стадий считается большим числом а сама обработка данных занимает от силы 2..3 стадии, но именно тот факт, что пиксели не зависят друг от друга, позволяет эффективно использовать столь длинные конвейеры в графике, скрадывая огромные латентности таких операций, как выборка текстур. Именно это можно назвать временным параллелизмом :-)

Однако гибкость современных графических алгоритмов растет. Появилось понятие зависимой выборки текстур - ситуации, когда координаты выборки определяются для каждого пикселя отдельно, возможно, прямо в пиксельном шейдере, на основе предыдущих выборок:

• Выборка значения текстуры 1.
• Вычисление координат для новой выборки.
• Выборка значения текстуры 2 по вычисленным координатам.
• Еще вычисления.
• Запись результатов.

В такой ситуации нас не спасет очень длинный конвейер. Приступив к выборке второго значения текстуры, мы не можем исполнять шейдер дальше до ее завершения, и нам придется ждать добрую сотню тактов, в течение которой мы даже не можем приступить к второй части вычислений («Еще вычисления» на схеме), т.к. они наверняка оперируют со значением, выбранным из второй текстуры, и должны дожидаться окончания выборки.

Что делать?

Решение есть - давайте снова обратимся к услугам временной параллельности. Создадим достаточно большую, скажем из более-чем сотни пикселов очередь, заранее подготовленных к обработке объектов. А далее будем брать одну команду шейдера и прогонять через нее ВСЕ наши пикселы, затем сохранять данные, полученные после ее исполнения (для этого нам понадобится большой пул, в котором мы будем хранить промежуточные данные вычислений для всей очереди). Затем мы будем брать вторую команду и снова прогонять через нее все наши пикселы и т.д. до завершения шейдера. Таким образом, мы получим ситуацию, когда команда может исполняться сотни тактов, но, при этом она может быть конвейеризована очень длинным конвейером, и он будет выдавать по результату за такт вне зависимости от того, ждут ли последующие команды шейдера результатов предыдущих. Т.е. задержка выборки текстур просто перестанет для нас существовать, как и задержка любой другой операции. Ведь у нас есть около сотни пикселов в деле, которыми мы можем заниматься в рамках одной команды (операции), прежде, чем дело дойдет до следующей.

Итак, мы имеем следующую схему:

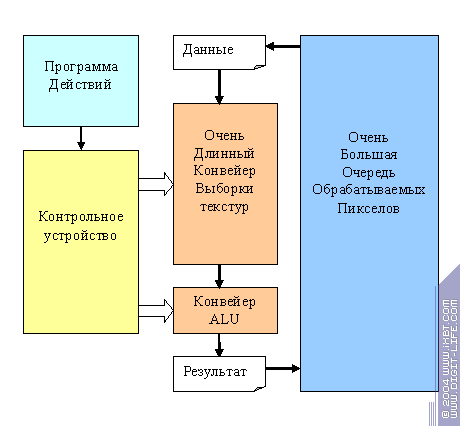
К этой схеме мы еще вернемся. А пока, для нас главным является тот момент, что именно независимость пикселов или вершин друг от друга позволяет нам эксплуатировать различные виды параллельной обработки, делая графический ускоритель столь эффективной машиной. Даже в случае относительно сложных процедур он способен каждый такт выдавать множество новых результатов.

Последний пункт, который мы затронем в нашей медитации, вопрос обеспечения исходными данными. Очень актуальный вопрос для столь деятельных и многопараллельных процессоров, коими являются графические. Как известно, технологии памяти развиваются не так стремительно, как вычислительная мощь, и только один приятный факт - потоковая природа графических алгоритмов - позволяет прокормить современные ускорители данными. Графический процессор похож на воронку - в нее поступает много разных данных, из него выходит только результирующее изображение. При этом, все поступающие данные по своей сути потоки, они считываются последовательно или почти последовательно, более менее удобным образом. А следовательно могут быть кэшированы, выбраны предварительно, помещены в очереди и т.д. - все для того чтобы подсистема памяти не простаивала и работала эффективно. К счастью в современных ускорителях практически нет произвольного доступа к памяти, ибо он, как известно, убивает эффективность кэширования. Поэтому, в отличие от обычных процессоров, кэши GPU относительно малы, раздельны, и работают, как правило, только на чтение. Это позволяет сделать их особенно эффективными - даже кэш буфера кадра можно разбить на две части, одна из которых работает только на чтение, а вторая является обычной очередью записи. Итак:

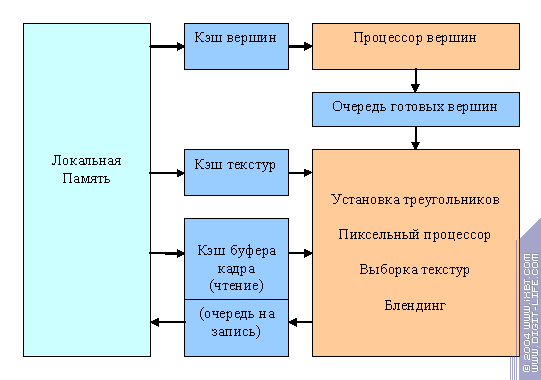
И вот именно на этой схеме наша медитация плавно перетекает в реальность.

Реальность и наши о ней догадки

А теперь, на примере современных DX9 семейств NV3X и R3XX мы посмотрим, как принципы нашей медитации реализовываются в жизнь. Или могут быть реализованы, т.к. многие детали архитектуры в этой статье остаются лишь нашей догадкой - разработчики ускорителей не желают вдаваться в подробности слишком далеко. И мы их понимаем: некоторые находки и подходы они с удовольствием скроют от своих прямых конкурентов. Читайте на свой страх и риск - мы ничего не гарантируем, но, согласитесь, на первый взгляд все выглядит логично и правдоподобно :

Cперва, чтобы понять, КАК все работает, обратимся к более удобной для восприятия логической структуре ускорителя (графический конвейер):

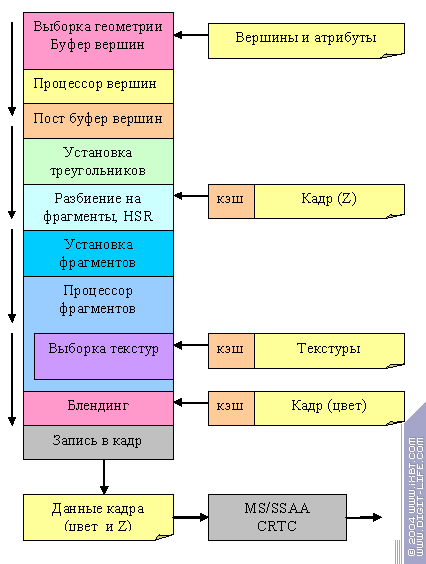
Итак, как происходит построение изображения:

1. Данные вершин выбираются из памяти и попадают в предварительный кэш вершин. Задача эта не так проста, как кажется на первый взгляд. Современные ускорители поддерживают несколько топологий хранения геометрии (треугольников) в памяти - такие как strips и fans, индексный буфер ( в котором для каждого треугольника указываются индексы трех его вершин из общего массива).

   Кроме того, поддерживается аппаратно гибкий формат данных - для каждой вершины могут храниться не только классические данные, такие как координаты или вектор ее нормали, но и любые другие наборы атрибутов допустимых скалярных или векторных типов. Есть аппаратная поддержка работы с несколькими потоками данных - когда часть атрибутов вершины храниться в одном массиве данных, а другая часть в другом. В таком случае выборка из памяти должна идти в несколько потоков. Всем этим и занимается блок выборки геометрии.
   
   

2. Далее, каждая из вершин попадает в вершинный процессор. Подробнее мы вернемся к нему чуть позже.
   
   
3. После вершинного процессора трансформированные и освещенные (т.е. уже обработанные вершинным шейдером или фиксированным T&L блоком) вершины попадают в небольшой (порядка 32-х вершин в современных архитектурах) промежуточный буфер. Он называется «Post T&L буфер вершин». Этот буфер играет двоякую роль, во-первых, служит для накопления результатов готовых отправиться на последующие стадии конвейера и таким образом уменьшает вероятность потенциальных простоев блоков ускорителя в ожидании данных, а во-вторых, позволяет избежать повторного трансформирования и обработки шейдером вершины, если она будет использована в скором времени повторно. Например, c соседним треугольником - такое происходит часто, несмотря на наличие разных подходов к описанию геометрии, практически в каждом из них одна вершина будет использоваться несколько раз.
   
   
4. Далее вершины объединяются по три, в соответствии с треугольниками, к которым они принадлежат, и отправляются в блок установки треугольников, где происходит предварительная подготовка данных, необходимых для закраски всего треугольника. Здесь же производится отбрасывание невидимых (вышедших за экран или заданные плоскости отсечения) и повернутых к нам обратной стороной (если такая опция задействована) треугольников.
   
   
5. Далее, треугольник разбивается на фрагменты, часть которых признается невидимыми и отбрасывается в ходе Z теста на уровне фрагментов (то, что мы называем HSR). Как правило, конечным результатом этого процесса являются видимые (или частично видимые) фрагменты 2х2 пикселя - т.н. «квады» подлежащие закраске. Именно такие фрагменты наиболее удобны для быстрой закраски пикселей (по нескольким, в основном математическим причинам, связанным с интерполяцией текстурных координат). Здесь мы остановимся подробнее:

   В современных ускорителях этот процесс построен в два этапа и во многом это связано с технологиями быстрой работы с буфером глубины - сжатия Z и иерархического контроля видимости. Современные ускорители, как правило, используют два уровня - блоки 4х4 (16 пикселей) - именно такими сжатыми блоками удобно хранить и сжимать в памяти Z буфер, и «квады» 2х2 - именно такими блоками происходит закраска в пиксельном процессоре. Итак:
   
   

   

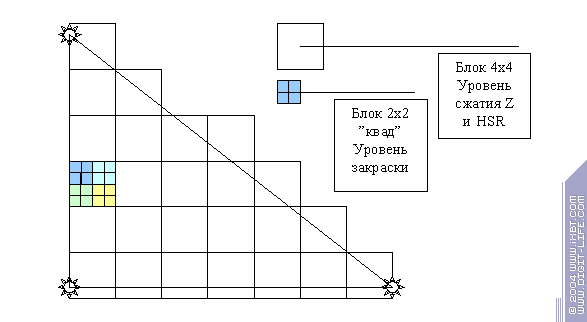
   на схеме проиллюстрирован процесс разбиения треугольника на фрагменты. Вначале, мы разбиваем его на большие фрагменты, причем они должны покрывать его целиком, даже если только один пиксель фрагмента принадлежит треугольнику, мы все равно будем считать его кандидатом на закраску. Для каждого фрагмента мы заранее вычисляем самую ближнюю Z координату всех его точек. Далее мы пытаемся определить, нельзя ли нам отбросить сразу весь блок 4х4. Для этого, мы используем специальный иерархический буфер глубины - еще один небольшой Z буфер, в котором хранится лишь одно, максимальное (самое дальнее) значение глубины для всего блока 4х4. Мы сравниваем это значение с ближней Z координатой всего блока. Если выясняется что все точки блока 4х4, которые мы собираемся закрасить, расположены дальше, мы можем признать весь блок невидимым и исключить его. Если нет - мы разбиваем его на 4 квада и для каждого из них вычисляем Z координаты. И только здесь нам приходит время обратиться к полному Z буферу, считав и распаковав из него блок 4х4 (если он еще не храниться в нашем кэше). Затем, мы сравниваем значения глубины и отбрасываем полностью невидимые квады (если такие будут) а остальные отправляем на установку и закраску в пиксельный процессор. При этом мы снабжаем их вычисленными значениями глубины и специальной битовой маской, которая говорит, какие из пикселей квада видимы а какие следует игнорировать (ведь часть квада может оказаться за гранью треугольника, а другая часть пикселей может быть невидима из за того, что не пройдет Z тест). В итоге мы пришли к следующему алгоритму:

   проверка глубины для блока 4х4 в малом вспомогательном Z буфере;
отбрасываем если весь блок дальше (не видим)

иначе

     считываем и распаковываем блок из основного Z буфера;
     проверяем каждый из квадов;
     отбрасываем если весь квад дальше (не видим)

     иначе

          проверяем каждый из пикселей квада, и
          выполняем операции с буфером шаблона (stencil), и
          снабжаем пиксели флагом видимости;
          устанавливаем, какие из них надо записать,
          а какие игнорировать;
          отправляем квад на установку и в пиксельный процессор;


Мда, как все непросто.

   Конечно, это зависит от приложения, но в среднем, как минимум половина пикселей будет отброшена еще до закраски. Поэтому, производительность проверки и вычисления Z должна быть выше максимальной производительности закраски. Так и есть - современные ускорители могут проверять на видимость (отбрасывать) 16 и более точек за такт. И, разумеется, вычислять больше значений глубины, чем закрашенных пикселей.
   
   

   Например, NV30/NV35/38, как известно способны вычислить, проверить и записать 8 значений глубины и буфера шаблонов за такт, но, при условии, что не происходит никакой работы с цветом (т.е. пиксельный процессор не функционирует). Подобная возможность заметно ускоряет некоторые алгоритмы построения изображений требующие отдельных проходов для предварительного вычисления глубины и буфера шаблонов. Пропускная же способность пиксельного процессора этих чипов ограничена одним квадом (4 пикселя) в такт. Кроме того, не забудем и про режим MSAA сглаживания, когда нам необходимо всегда вычислять вдвое или вчетверо больше значений глубины, а вот значение цвета по-прежнему вычисляется только одно.

   Еще один интересный аспект реализации - маленький буфер глубины, используемый нами для предварительного определения видимости блоков 4х4. Этот же буфер используется и для технологии быстрой очистки буфера глубины - достаточно записать в него специальное значение, делающее содержимое основного буфера в локальной памяти «неликвидным».
   
   

   Известно, что в семействе R3XX он полностью хранится на чипе (!), и именно поэтому в свое время продавались более дешевые варианты карт с чипами, на которых эта функция была отключена - таким образом некоторые отбракованные кристаллы шли в дело (помним RADEON 9500 и попытки переделок его в RADEON 9500 PRO/9700, а также с RADEON 9800SE похожая ситуация). Есть подозрение (не подтвержденное официально, но вполне логичное), что и некоторые чипы NV3X держат подобный мини-буфер на кристалле, целиком, или как минимум достаточно крупными кусками. Это может быть одной из причин, по которой NV34 (в нем подобная функциональность раннего отсечения фрагментов по глубине отсутствует), обходится меньшим числом транзисторов, не смотря на схожую с NV31/NV36 формулу 4х1.

   Как известно, R3XX закрашивает сразу 2 квада (т.е. может выдавать до 8 цветных пикселей за такт), и отбрасывает по некоторым данным до 64 невидимых точек за такт, т.е. четыре блока 4х4(!). Но, в отличие от NV3X, не умеет записывать больше 8 значений глубины и буфера шаблонов.
   
   

6. Далее фрагменты 2х2 (квады) отправляются на установку фрагментов. Здесь для каждого из них вычисляется (интерполируется) множество необходимых параметров, таких как текстурные координаты, MIP уровень, векторы и установочные параметры анизотропии и т.д. Именно здесь факт блока 2х2 играет свою оптимизирующую роль - вычисляются только базовые значения параметров на весь блок и специальные коэффициенты dx и dy - их предполагаемое отличие (производная) по горизонтали и вертикали блока. А затем, из одного набора параметров получаются все 4:
   
   
   
   
   

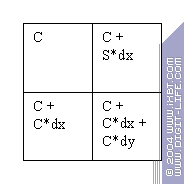
   Зачем такие сложности? Дело в том, что по мере роста сложности пиксельных шейдеров растет и число передаваемых и интерполируемых для каждой точки параметров. Число интерполяторов в чипе не может быть очень большим - это достаточно емкая вычислительно операция, и интерполяция типичного набора параметров может занимать более одного такта, замедляя закраску. Использование квадов позволяет существенно (в разы), поднять эффективность этого процесса.

   Интересно, что в практических реализациях процесс интерполяции параметров может частично или полностью проходить в пиксельном процессоре, используя его специальные или общие ресурсы (ALU).
   
   

7. После установки и интерполяции параметров происходит закраска фрагментов. Об этом мы поговорим чуть позже подробно, пока же отметим, что существенной частью этого процесса является выборка и фильтрация текстур.
   
   
8. После того как значения цвета были рассчитаны, в пиксельном процессоре происходит смешение (блендинг) - если включен соответствующий режим - или просто запись результирующих значений цвета и глубины в буфер кадра. На этом этапе может происходить несколько дополнительных операций, таких как: гамма-коррекция или вычисление самого дальнего значения Z всего блока 4х4 для корректного обновления мини-буфера глубины, сжатие Z координат и т.д.
   
   
9. После того как изображение построено, может быть произведен дополнительный проход для усреднения результатов полноэкранного АА, иногда этот процесс сразу совмещен с выводом на экран.

Теперь, настало время подробнее вернуться к вершинным и пиксельным процессорам, но сперва, обсудим несколько тонкостей практической реализации. Вот так выглядит блок схема современного ускорителя приближенная к его практической реализации:

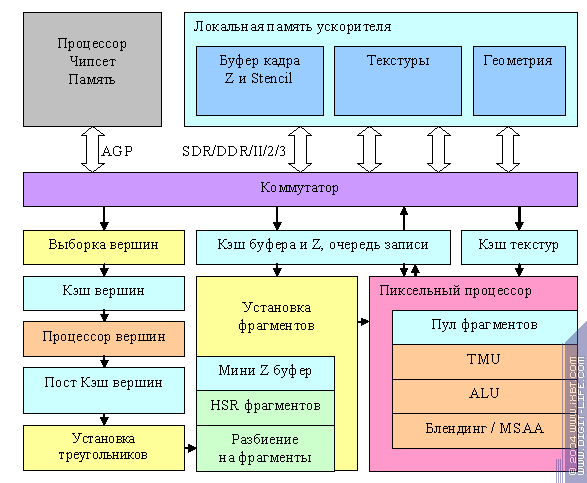
Во-первых, обращает на себя внимание многоканальный контроллер памяти. Вместо одной очень широкой 128- или 256-бит шины памяти используются 2 или 4 полностью независимых (разведены отдельные управляющие сигналы) шины памяти шириной 32 или 64 бита соответственно. Зачем это сделано? Давайте посмотрим внимательно на потоки данных, которые идут во время работы ускорителя. Текстуры, как правило, только считываются. Геометрия, тоже как правило, только считывается. Буфер кадра (цвет), как правило, только записывается. Буфер глубины (Z) - считывается и записывается. На лицо как раз 4 непрерывных потока данных. Если мы сумеем разнести их (хотя бы частично) по разным контроллерам, то мы получим многократный выигрыш с точки зрения времени задержки при обращении к данным. Нам не придется регулярно переключать память из режима чтения в режим записи и скакать по ней от буфера к буферу. А это значит, что мы можем сделать очень небольшие и эффективные кэши! Типичные размеры (получены экспериментально или предположены):

• Кэш вершин: ~50..100..200 вершин;
• Пост Кэш вершин: ~16..32 вершины;
• Кэш текстур: ~32..64 килобайт (~512 блоков 4х4);
• Кэш буфера кадра и глубины: 16..32 килобайт (~256 блоков 4х4);
• Минибуфер глубины: ~256 килобайт максимум, скорее всего меньше;

В этом кроется важное отличие графических ускорителей от процессоров. Потоковый и предсказуемый характер данных позволяет обходиться небольшими КЭШами высокой эффективности. Данные (буфер кадра, буфер глубины, текстуры) зачастую хранятся и выбираются прямоугольными блоками, что повышает эффективность работы с памятью. Основная масса транзисторов уходит на многочисленные ALU и длинные конвейеры, что существенно ограничивает тактовые частоты - синхронная работа сложного специализированного конвейера длиною более чем в 100 стадий требует существенных допусков на неравномерное распространение сигналов. Именно поэтому характерные для CPU частоты в несколько гигагерц пока недостижимы для графических ускорителей, даже при более тонкой технологической норме.

И, наконец, самое интересное:

Вершинный процессор

Суммируем наши знания о современных вершинных процессорах:

	DX9 2.0	R3XX	NV3X
Версия шейдеров	2.0	2.0	2.X*
Статические ветвления	Да	Да	Да
Динамические ветвления	Нет	Нет	Да
Вложенные циклы и подпрограммы	Нет	Нет	Да
Входных регистров (атрибутов вершины)	16	16	16
Плавающих константных регистров	128	256	256
Целых константных регистров	16	16	**
Логических константных регистров	16	16	**
Счетчик цикла	1	1	**
Временных регистров	12	16	32
Адресных регистров	1	1	2
Предикаты	Нет	Нет	1
Выходных параметров (координат текстуры)	8	8	8
Задание плоскостей отсечения	Нет	Нет	Да
Задание цвета второй грани	Нет	Нет	Да
Код шейдера, длинна, ассемблерных команд	256	256	256
Ассемблерных команд выполняется, до	65536	65536	65536

*) 2.X в терминологии DX9 означает 2.0 + дополнительные возможности;

**) аппаратура NV3X позволяет использовать для этих целей любой плавающий константный регистр, без каких либо ограничений, и таким образом не только эмулирует эту функциональность но и предоставляет больше.

Прокомментируем эту таблицу.

• Версия шейдеров - официально поддерживаемая в DX9 версия шейдеров (некоторая дополнительная функциональность NV3X доступна только в OpenGL, например второй адресный регистр).
• Статические ветвления - ветвления циклы и подпрограммы, зависящие только от заданных извне шейдера констант.
• Динамические ветвления - ветвления, циклы и подпрограммы на основе принятых прямо во время исполнения шейдера решений (как в CPU)
• Вложенные циклы и подпрограммы - возможность исполнять оные.
• Входные регистры - плавающие векторные 4D регистры, в которые попадает исходная информация об обрабатываемой вершине, выбираемая ускорителем из памяти.
• Константные регистры - могут быть заданы извне, из приложения, но не могут быть изменены во время исполнения шейдера.
• Счетчик цикла - векторный регистр хранящий минимальное, максимальное и текущее значение итерации цикла. У чипов NV3X его роль может исполнять любой константный регистр, причем нет ограничений на вложенность циклов - соответственно могут быть задействованы несколько счетчиков одновременно.
• Временные регистры - плавающие векторные регистры общего назначения для промежуточных рассчетов.
• Предикаты - разновидность динамических условий - некий флаг, который задается предварительно как результат того или иного сравнения, и затем может влиять на исполнение команд, помеченных специальным образом. Если команда помечена предикатом, то результат ее исполнения будет отброшен - если флаг находится в одном состоянии, и будет засчитан - если в другом. Таким образом, можно реализовывать небольшие условия, не прерывая потока команд (что зачастую более выгодно, в случае наличия конвейера). Приведем пример. Вот такой алгоритм:
  если а>1 то b=a*2 иначе b=a;
  может быть записан с помощью предикации как:
  установить предикат если a>1;
предикат(истина) b=a*2;
предикат(ложь) b=a;

  причем каждая строчка соответствует лишь одной команде вершинного процессора, т.к. условие предиката является ее частью.
• Выходные параметры - 8 четырехмерных плавающих регистров, которые и интерполируются по поверхности закрашиваемого треугольника (см. установка квадов ранее) и попадают затем как входные параметры в пиксельный шейдер при закраске каждого пиксела.
• NV3X имеет полезную возможность определять 6 плоскостей отсечения в вершинном шейдере для каждой вершины персонально, а также задать не только два основных цвета интерполируемых по поверхности треугольника, но и два отличных цвета для обратной грани треугольника.

В общем и целом, становится видно, что в то время как вершинный процессор R3XX практически один в один реализует стандарт 2.0, оный же у NV3X лишь немного не дотянул до возможностей вершинных шейдеров 3.0. О самих 3.0 мы еще подробно поговорим в статье DX Next, а здесь лишь отметим, что главное отличие, по той или иной причине не реализованное в аппаратуре (или внесенное в спецификацию 3.0) - возможность доступа к текстурами из вершинного шейдера.

Есть и другие отличия в реализации - такие тонкости, как аппаратная поддержка вычисления SINCOS или EXP (в базовом DX9 они заменяются макросами из нескольких команд), но мы не будем вдаваться в детали так глубоко, что за деревьями вдруг станет не видно леса. Основное отличие, как не крути - динамическое управление исполнением шейдера на NV3X.

Очевидно, что для реализации вершинного процессора R3XX можно избрать схему с общей контрольной логикой, и несколькими параллельно работающими ALU, синхронно обрабатывающими несколько вершин по одной и той же программе. Нет ни динамических переходов, ни предикатов, константы не изменяются и могут быть использованы совместно. Вот так выглядит вершинный процессор старших моделей R3XX:

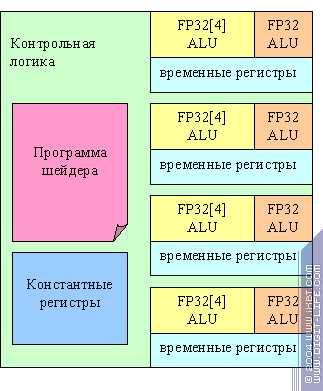
Кроме общей контрольной логики и разделяемых констант, отметим наличие двух ALU - векторного четырехмерного и скалярного. ALU могут работать параллельно, выполняя таким образом до двух различных математических операций за такт. Столь странная конфигурация (пять ALU по схеме 4+1 а не четыре по схеме 3+1) видимо была изначально продиктована необходимостью быстро выполнять скалярное произведение, а затем, обобщена до полноценного суперскалярного исполнения. На младших чипах линейки (RV3XX) присутствует два набора ALU и регистров вместо четырех.

По идее, NV3X должна содержать раздельные, независимые вершинные процессоры - наличие динамического управления исполнением как минимум хороший повод предположить это. Однако, реально многое указывает на совершенно иную картину. Вершинный процессор NV3X близок к тому, что мы увидели в последнем чипе 3dlabs. Попробуем нарисовать его предполагаемую схему:

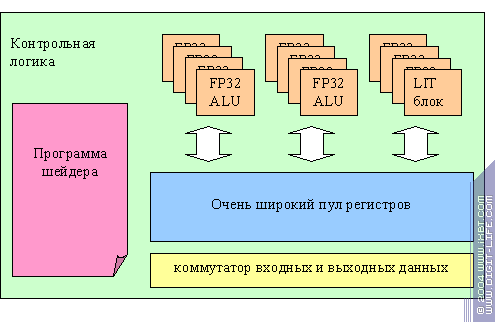
Озвучим свои догадки. Фактически у нас есть очень широкий массив независимых скалярных плавающих ALU, очень широкий пул регистров и программа шейдера, записанная в виде VLIW микрокода, указывающего для каждого следующего такта действия сразу для всех ALU. В чем преимущество и недостатки такого подхода? С одной стороны мы можем оптимально распределить вычислительные ресурсы, обрабатывая несколько вершин. В том числе и максимально плотно задействовать все ALU путем трюков с компиляцией микрокода, в котором одновременно исполняются одни операции для одной вершины и другие для другой. В случае меньшей сложности шейдера мы можем одновременно обрабатывать больше вершин (высвобождаются регистры). Нам легче включить в эту схему специализированные аппаратные блоки, например для ускорения фиксированного T&L. С другой стороны как же быть с гибкостью? Ведь мы не можем дирижировать всей этой оравой устройств раздельно, в несколько потоков, в зависимости от динамически вычисленных условий. Здесь есть два выхода: во-первых, мы можем построить все динамические условия на предикатах, снабжая каждую строку VLIW микрокода набором из 4 или даже более предикатов и заведя соответствующие регистры. Во вторых, мы можем пойти дальше, реализовав в контрольном устройстве несколько счетчиков команд (несколько потоков инструкций), например 2, но в большинстве шейдеров, не имеющих динамического контроля исполнения или переходов, вообще использовать только один поток команд, но зато с наибольшей эффективностью и над наибольшим числом вершин. Что поделать, мы не знаем, какова истина, но, как минимум, привели свои соображения на этот счет. Масштабирование вершинного процессора NV3X в младших чипах можно выполнять очень тонко - достаточно начать сужать пул регистров и уменьшать число ALU и функциональных блоков.

Сотрудники NVIDIA говорят, что производительность вершинного процессора NV31 и NV34 в 2.5 раза медленнее, чем у старших моделей. В NV36 вершинный процессор взят из NV35 без каких-либо изменений (!), и его производительность бескомпромиссна. Зачем это сделано? Очевидно, что для игровой mainstream карты она чрезмерна, но мы не будем забывать что на основе тех же самых чипов делаются и профессиональные решения NVIDIA, Quadro FX, а там вершинная производительность зачастую играет решающую роль. C другой стороны, по сравнению с процессором фрагментов вершинный процессор занимает не так много транзисторов, и можно позволить себе включить в среднее по цене решение самый производительный вариант.

Пиксельный процессор (процессор фрагментов)

Начнем опять таки с таблички:

	DX9 2.0	R3XX	NV3X
Версия шейдеров	2.0	2.0	2.X*
Аппаратно поддерживаемые форматы	FP	FP24	I12 FP16 FP32
Различных текстур (сэмплеров)	16	16	16
Входных регистров (текстурных координат)	8	8	8
Входных регистров (значений цвета)	2	2	2
Плавающих константных регистров	32	32	512*
Временных регистров	12	32	32
Предикаты	Нет	Нет	1
Выходных регистров (цвет)	1**	4	1***
Код шейдера, длинна, ассемблерных команд	96	160	1024
Команд доступа к текстурам, исполняется, до	32	32	1024
Команд арифметических исполняется, до	64	64+64****	1024

*) Фактически, константы хранятся в самом коде шейдера и каждая использованная константна, уменьшает доступное число команд.

**) От 1 до числа поддерживаемых одновременно буферов рендеринга MRT (т.е. до 8)

***) Реально выходной регистр это один из временных регистров, в отличии от R3XX где он существует отдельно. Таким образом, эффективное число временных регистров на NV3X меньше.

****) до 64 векторных и до 64 скалярных, но с некоторыми условиями (см. далее)

• Версия шейдеров - официально поддерживаемая в DX9 версия пиксельных шейдеров (опять таки, некоторая дополнительная функциональность NV3X доступна только в OpenGL, например одновременное исполнение плавающих и целочисленных операций).
• Аппаратно поддерживаемые форматы - те форматы данных, с которыми реально оперируют ALU процессора фрагментов.
• Различных текстур (сэмплеров) - сколько всего различных текстур может быть адресовано из одного шейдера. Отметим, что даже имея меньшее число интерполируемых текстурных координат, мы можем выбирать данные из нескольких текстур пользуясь одним вектором координат, или вычислить необходимые координаты прямо в шейдере.
• Входные регистры - интерполированные для каждого пикселя значения двух цветов и 8 текстурных координат (в т.ч. с перспективной коррекцией).
• Плавающих константных регистров - константы, загружаемые в пиксельный шейдер из приложения. В NV3X не существует отдельных аппаратных регистров для констант - они хранятся в теле микрокода шейдера, занимая отведенные под инструкции слоты. Одна константа занимает место двух инструкций, и, таким образом, их число не может превысить 512. Интересно, что сама программа пиксельного шейдера хранится в чипах NV3X в локальной памяти и подгружается оттуда по мере исполнения. А вот код вершинного шейдера всегда находится в ускорителе.
• Временные регистры - плавающие векторные регистры общего назначения для промежуточных рассчетов.
• Предикаты - пиксельный процессор NV3X поддерживает предикацию - т.е. даже в пиксельных шейдерах мы можем принимать решения динамически.
• Выходных регистров - ATI поддерживает MRT - можно записывать результаты в четыре одинаковых буфера со значениями цвета одновременно. NVIDIA не поддерживает эту возможность (один из самых досадных моментов), но позволяет запаковывать несколько значений специальными инструкциями, выводя в итоге одну структуру данных произвольного содержания, не превышающую 128 бит на пиксель (FP32[4]). Однако отметим, что на запаковку и распаковку тратятся инструкции пиксельного шейдера, а это не лучший сценарий для практических задач.
• Число команд. NV3X позволяет исполнять до 1024 любых команды, в любой последовательности, с любым числом доступов к текстурам и любой степенью вложенности зависимых выборок (когда значение из текстуры используется для вычисления новых координат доступа к следующей текстуре). В случае ATI все гораздо проще аппаратно и потому гораздо сложнее с точки зрения программиста. В общем и целом мы можем осуществлять 32 доступа к текстурам, но степень вложенности не должна превысить 4. Можно использовать до 64 арифметических векторных команд и до 64 скалярных команд, но, эти дополнительные скалярные вычисления спариваются с векторными по схеме 3+1, и любая четырехмерная векторная команда уже не может быть спарена со скалярной.

Итак, с точки зрения спецификации и гибкости NV3X выглядит лидером. Однако, как мы хорошо знаем, что на практике, с точки зрения производительности в пиксельных шейдерах 2.0 все наоборот. За сложность приходится платить не только длительной отладкой и оптимизацией компилятора в драйверах (последний заметный прирост скорости шейдеров был несколько месяцев назад), но и просто пиковой производительностью.

А теперь самое интересное. Упрощенная схема конвейера процессора фрагментов NV35 (мы не приводим многие детали, т.к. они ничего не добавляют к описанию сути происходящего процесса):

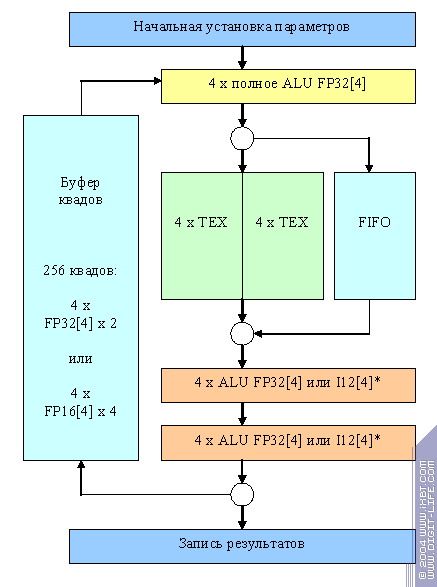
Как все это работает? Одновременно в обработке находится несколько сотен (!) квадов 2х2. В контексте процессора фрагментов квад представляет собой структуру данных, содержащую для каждого из четырех пикселей следующую информацию:

• Флаг активности данного пиксела (вспоминаем, что не все точки квада могут быть видимыми);
• Флаг значения предиката для данного пиксела;
• Значение Z и возможно значения буфера шаблонов;
• Два векторных временных регистра FP32[4] которые могут быть разделены на четыре FP16[4].

Все обрабатываемые квады по очереди проходят через этот длинный конвейер, состоящий из ALU, затем двух текстурных модулей и затем еще двух ALU. Длина конвейера (и соответственно время прохода квада через него) более двух сотен тактов. Большая часть которых (~170) приходится на операцию выборки и фильтрации текстур и скрыта в текстурных блоках. В нормальном режиме работы конвейер способен выдавать по кваду за такт.

Итак, за один «оборот» этой гигантской карусели, для каждого из 4 пикселей квада могут быть осуществлены (или не осуществлены) следующие операции:

• Полное ALU - одна четырехмерная векторная операция любой сложности из доступного набора (превышает спецификации PS 2.X) в формате FP32 или FP16
• Выборка и фильтрация двух значений текстур
• Упрощенные ALU (на схеме помечены *) - две простые векторные операции (сложение, умножение) в плавающем формате или в формате I12, а также любая из операций соответствующая функциям комбайнеров (стадий) FFP.

Затем, если двух выборок текстур и трех операций было недостаточно, квад может отправиться по кругу, через буфер квадов, заново на вход этого конвейера. В режиме совместимости со старыми приложениями (FPP и шейдеры до 1.3 включительно) используются целочисленные возможности мини ALU, а плавающее ALU помогает рассчитывать и интерполировать текстурные координаты. В этом случае двух временных регистров на пиксел всегда хватает (рамки спецификации).

Теперь посмотрим, как построено исполнение шейдеров 2.0 (и 1.4).

Из локальной памяти карты выбираются одна за другой команды микрокода пиксельного шейдера. Одна строчка микрокода конфигурирует весь конвейер, включая по два модуля выборки и фильтрации текстур и по 3 ALU одинаково настраиваемые для каждого из четырех пикселов квада. Затем, все квады по очереди проходят через этот конвейер. Затем, конвейер конфигурируется на новый набор операций и все повторяется. Таким образом, существенная работа ложится на компилятор шейдера - он должен постараться собрать команды шейдера в как можно более плотно использующие ресурсы конвейера пачки. Код шейдера:

1. Вычисления
2. Выборка текстуры 1
3. Вычисления с ее результатами
4. Выборка текстуры 2
5. Вычисления координат по результатам 2 выборки
6. Выборка текстуры 3 по вычисленным координатам
7. Вычисления результата
8. Вычисления результата
9. Запись результата

Будет сгруппирован в две строчки микрокода (в скобках номер строки исходного шейдера):

1.  
         ALU: Вычисления (1)
         TEX1: Выборка текстуры 1 (2)
         TEX2: Выборка текстуры 2 (4)
         Мини ALU1: Вычисления с результатами TEX1 ()
         Мини ALU2: Простаивает (не годится для выполнения сложной операции 5)
   
   
2.  
         ALU: Вычисления координат по результатам второй выборки (5)
         TEX1: Выборка текстуры 3 по вычисленным координатам (6)
         TEX2: простаивает
         Мини ALU1: Вычисления результата (7)
         Мини ALU2: Вычисления результата (8)
   

Эффективность поражает - шейдер из девяти строчек был уложен всего в два такта. Однако тут есть свои подводные камни:

• Мини-ALU способны делать только некоторые операции, иначе они будут простаивать. В реальных 2.0 шейдерах это случается довольно часто. В 1.4 заметно реже, там, как правило, работают все ALU и именно поэтому результаты тестов так разительно отличаются.
• Выборки текстур должны происходить независимыми парами, иначе один текстурный модуль будет простаивать
• Желательно чтобы операции выбора двух текстур и математические операции чередовались, причем в зависимости от сложности по схеме 2+1, 2+2 или 2+3.
• Существенное влияние на производительность оказывает вопрос временных переменных

Последний вопрос требует пояснений. Дело в том, что во время вычислений используются временные регистры. Формально их 32, но реально, по ходу тех или иных операций используется, как правило, 2..4 временных регистра. И для NV3X здесь кроется огромная разница. Ведь если мы хотим объединить наши команды в одну строчку микрокода и обеспечить их исполнение за один такт мы должны позаботиться чтобы все они использовали в сумме не более двух FP32[4] (или четырех FP16[4]) временных переменных. Вот где кроется существенная разница производительности FP16 и FP32 на чипах серии NV3X - дело не в ALU, а в числе доступных временных переменных. Ведь если мы выходим за рамки двух или четырех переменных, нам придется совершать еще один оборот карусели, разбивая пачку команд на две, а это дополнительный такт. Или, что в некотором роде эквивалентно, нам придется задействовать две структуры квада для представления одного реального. Это опять таки увеличит число тактов вдвое. Вот почему NV3X так чувствительна к ручной оптимизации кода шейдеров и качеству встроенного в драйверы компилятора. Необходимо хорошо представлять архитектуру процессора фрагментов для того чтобы писать эффективно исполнимые шейдеры. В случае ATI R3XX архитектура значительно проще (см. далее) и для написания эффективного шейдера достаточно простого набора правил. Но, и максимальное число выполняемых за такт операций меньше.

Интересно, что приведенная нами схема процессора фрагментов NV35 (и соответственно NV38) являлась «работой над ошибками». Вот так (предположительно) выглядела схема NV30

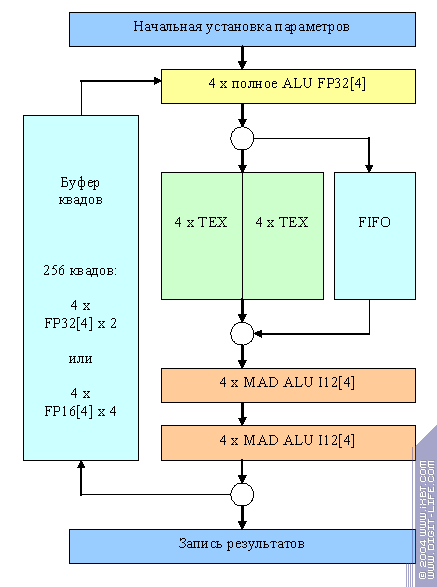
Мини-ALU были только целочисленными! Хотя и более производительными - плавающая арифметика, как известно, требует больше ступеней конвейера, и

целочисленные мини-ALU тратили тогда еще свободные ступени с пользой. Они умели исполнять MAD операцию, т.е. сложение и умножение одновременно. С одной стороны это позволяло порой показывать более высокие (в расчете на такт) результаты в FFP и PS1.1, с другой, результаты в PS2.0 почти всегда были более низкими. Видимо, разрабатывая NV3X делали ставку в первую очередь на производительность в DX8 приложениях, достаточно справедливо полагая, что в реальных приложениях (не тестах) PS 2.0 будет распространяться медленно. Однако отрицательное мнение обозревателей и просто энтузиастов во многом подогретое слабой производительностью вторых шейдеров стало толчком к проведению такой «работы надо ошибками» по замене целочисленных ALU на плавающие.

Теперь поговорим об урезанных версиях чипов. Вот так, предположительно, выглядит NV31

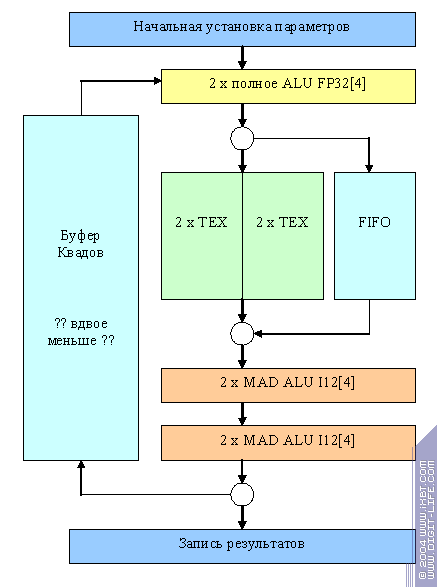
В большинстве случаев чип работает как 2х2, т.е. оперирует некими «полуквадами», по крайней мере, во время прохода их через конвейер, имеющий вдвое меньше ALU и текстурных блоков. Однако, предусмотрен и специальный режим коммутации 4х1 достижимый только в случае отсутствия «карусели» (т.е. зацикливания):

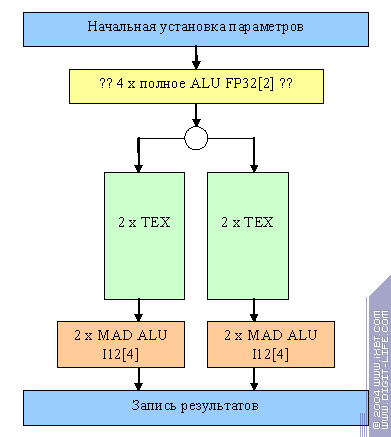
Он годится для простых задач закраски одной текстурой (небо и т.д) требующих от пиксельного процессора много филрейта и мало интеллекта. Собственно говоря, это и есть основной класс задач, когда конфигурация 4х1 будет смотреться выигрышнее конфигурации 2х2.

Соответственно NV36 отличается от NV31 другими мини ALU, как и в случае с NV35/38.

Теперь приведем предполагаемую схему пиксельного процессора R3XX. Фактически, в чипе присутствует два независимых процессора квадов, они работают асинхронно и более того, один может быть выключен (таким образом, блокировкой одного неработающего или работающего процессора квадов и получались обрезанные варианты чипа известные как 9500). Итак, один из двух процессоров R3XX:

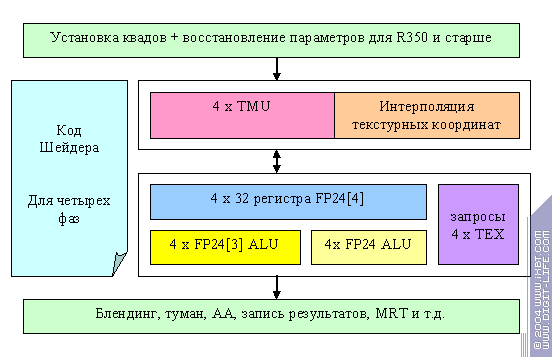
Самое главное отличие - процессор фрагментов действительно похож на процессор. А не на один большой цикл : как в случае NV3X. Процессор выполняет

операции шейдера, за один такт над четырьмя пикселами может быть выполнено до трех операций. Две арифметических (по схеме 3+1) и одна операция запроса значения текстуры. Однако, если арифметические операции мы выполняем быстро, мы не можем каждый раз ждать более сотни тактов выборки и фильтрации текстур. Поэтому, большое число обрабатываемых одновременно квадов присутствует и здесь, пусть и не так явно. Шейдер разбивается на 4 независимых фазы (микрокод каждой из них храниться прямо в пиксельном процессоре, отсюда и ограничение на глубину зависимой выборки текстур) и каждая из фаз исполняется отдельно. По ходу исполнения фазы накапливаются запросы к текстурному процессору. Таким образом, некое число одновременно обрабатываемых квадов (с точки зрения пиксельного процессора они обрабатываются последовательно) до четырех раз обращается к текстурному процессору с пакетом заданий. Судя по всему это число квадов существенно ниже того, что мы наблюдали у NV и, соответственно, размер очереди значительно меньше. Расплата - потенциальная задержка при зависимых выборках текстур. Бенефис - существенно более простая схема конвейера, возможность сделать больше конвейеров, нет таких жестких проблем с временными регистрами.

Можно долго спорить что лучше - приличная производительность на практически любом, написанном в «лоб» в соответствии с общими принципами DX9 шейдере (ATI) или более высокая производительность на специально оптимизированном под конкретное железо шейдере (NV) при риске в разы меньше производительности на неудачном с точки зрения компилятора коде. В сумме, с учетом 8 пиксельных конвейеров R3XX, ATI выиграла этот этап сражения, по крайней мере, на поле пиксельных шейдеров 2.0. Результаты тестов наглядно это демонстрируют. В области 1.4 и тем более 1.X NV3X показывает себя заметно лучше.

Очевидно, что уроки настоящего будут учтены в будущих поколениях (NV4X и R4XX). В первую очередь можно надеяться на решение проблемы (читай увеличение числа) временных регистров у NV и увеличение числа ALU у ATI.