Как физик, я готов признать, что в неких разумных рамках скоростей масс и энергий прямую можно считать наикратчайшим расстоянием между двумя точками. Но, как лирик, напомню, что наиболее красивым расстоянием между двумя точками остается кривая, причем гладкая и желательно как минимум третьего порядка. Несомненно, что трехмерные модели, заданные в виде кривых, выглядят более реально, нежели полигональные, особенно, если начать разглядывать их вблизи. Кстати, все относительно, ведь прямая — это параметрическая кривая первого порядка :-).
Мат-история
Но вот беда, с точки зрения реализации кривые страшно неудобны. Давайте, раз уж заговорили об этом, разберемся, почему именно. Для начала надо определиться с понятием кривой. Не будем погружаться в дебри математики, а просто положим, что кривой Kn (порядка n) в трехмерном пространстве является совокупность точек (траектория), однозначно задать которую можно следующим образом:
т.е. как набор из трех полиномов n степени от некой общей переменной (параметрическое задание). Соответственно, если полигоны первой степени, то мы получаем прямую, если второй, то так называемую "квадратную" кривую, если третьей, то кубическую.

Полиномы, степенью превышающие 3, применяются крайне редко, по крайней мере, в компьютерной графике. В основном, по соображениям вычислительной эффективности.
Соответственно, имея три полинома n степени, мы должны задать 3*(n+1) коэффициентов для того чтобы однозначно определить кривую. Отметим, что работать с бесконечными кривыми не очень удобно, да и в большинстве случаев не надо, поэтому параметр t, как правило, ограничивают неким стандартным диапазоном значений (обычно 0..1). Заданные таким образом кривые называются ограниченными кривыми или сегментами. Хранить и обрабатывать кривые, записанные в исконном виде (полиномами), крайне неудобно — для задания и манипуляций с кривой предпочтительнее определять ее в виде набора точек в пространстве, тем или иным образом "наглядно" задающего вид кривой:

Соответственно, необходимо иметь формулы для пересчета координат n+1 точки в коэффициенты. Кроме того, для того, чтобы эти формулы обеспечивали однозначное соответствие, хотелось бы еще иметь гладкую стыковку сегментов. А именно, взяв некий набор из k точек:
сгруппировав их следующим образом:
и построив по каждой четверке свой сегмент кривой, мы получим не только непрерывную, но и гладкую (математически говоря, с не равными нулю в месте стыковки сегментов производными первого порядка) суммарную кривую. Такое представление позволит нам удобно манипулировать данными и описывать кривыми различные, простые и сложные линии.
Теперь давайте повторим все предыдущие рассуждения, заменив кривую поверхностью, одну переменную t на две (скажем u,v) и полиномы на произведение двух полиномов заданной степени от этих переменных. Для задания подобной структуры в трехмерном пространстве нам понадобится уже 3*(n+1)*(n+1) чисел или, соответственно (n+1) в квадрате точек. Т.е. 16 точек (сетка 4*4) для поверхности третьего порядка (бикубической). Приставка "би" напоминает нам о том, что наша поверхность задается кубическими полиномами по каждому из двух параметров.
И снова, в случае бикубических поверхностей мы можем найти такое преобразование, которое позволит не только наглядно задавать, но и гладко стыковать сегменты. Сами преобразования (т.е. методы задания кривых поверхностей контрольными точками с соблюдением некоторых условий) носят хорошо знакомые специалистам имена — (B-Spline, Bezier Surfaces). Набор точек и параметров, однозначно задающих сегмент, принято называть патчем (Patches).
С высот теории в болото практики
Все, что описано ранее, требует массу вычислений. Самый неприятный момент — отрисовка сегментов. Если для стандартного примитива современных акселераторов — треугольника мы можем построить однозначное соответствие точка экрана — текстура/параметры освещения, и быстро закрасить его, используя инкрементальные алгоритмы (грубо говоря, по одному сложению и умножению на параметр для каждой точки), то с поверхностями второго и тем более третьего порядка все не так просто. Во-первых, мы не можем найти однозначного соответствия между точкой экрана и точкой на поверхности — как известно, уравнение степени выше единицы может иметь разное число решений, в том числе большее 1, либо не иметь их вовсе. Т.е. в случае бикубической поверхности на одну точку экрана могут претендовать до 3 точек поверхности включительно. Нахождение которых задача нетривиальная (с множеством условий) и вычислительно невыгодная. Я думаю, все решали в школе уравнения третьего порядка и помнят, насколько это сложнее квадратных уравнений. А здесь нам предстоит решить систему из нескольких таких уравнений. Реализовывать это в железе для каждой точки крайне расточительно. Поэтому принято поступать несколько иначе — разбивать сегмент поверхности равномерной сеткой, вычислять промежуточные точки и рисовать поверхность в виде набора треугольников на основе этих точек. Этот процесс называется тесселяцией — разбиением примитива более высокой степени на набор примитивов более низкой. В нашем случае — поверхность приближается набором треугольников. Ранее подобные операции лежали на плечах процессоров и приложений, но сейчас они постепенно приходят на уровень драйверов, ускорителей и API:

например, NVIDIA GeForce3 способен аппаратно тесселировать прямоугольные патчи, и поддержка этой возможности есть в DirectX 8. Плюсы и минусы в студию:
Плюсы:
- В случае аппаратной реализации тесселирования резко снижается нагрузка на AGP и шину памяти — мы храним и передаем небольшое количество геометрической информации, а в результате получаем детальную поверхность из множества треугольников.
- Легко реализовать отрисовку моделей, заданных подобным образом, с адаптивным (в зависимости от расстояния до модели) уровнем детализации — мы просто меняем число треугольников, на которое ускоритель разбивает сегмент.
- Мы полностью задействуем мощь современных ускорителей и, в первую очередь, их T&L блоки, не упираясь в слабый центральный процессор системы.
- Большое число треугольников позволяет организовать освещение и тени без использования карт освещения, полностью переложив заботы об оном на шейдеры и T&L. Подобный подход позволит создать невероятную динамическую среду — все предметы будут отбрасывать тени, все источники света смогут двигаться по произвольным траекториям. Исчезнет необходимость в длительных предварительных расчетах.
Минусы:
- Фактически придется иметь две версии описания мира и моделей в игре — заданные в виде кривых для ускорителей, которые поддерживают аппаратную тесселяцию, и в виде прямых для тех, которые не поддерживают. В DirectX 8 программная эмуляция этой функции недоступна.
- Практически нереально переработать уже написанное обеспечение, ориентированное на треугольники.
- Процесс создания и редактирования моделей, состоящих из поверхностей, заданных подобным образом, не столь удобен и отработан, как в классическом случае.
На данный момент, минусы существенно перевешивают, казалось бы, феерические достоинства, причем, основную роль играет первый, "коммерческий" пункт. Пока никто не спешит продавать и создавать игру, годную только для GeForce3.
Истинные формы
В скором времени на рынок должен выйти конкурент GeForce3 — чип нового поколения от ATi с кодовым именем R200. Чтобы на что-то надеяться, ATi должна предложить решение не равное, но технологически превосходящее NVIDIA. Голая производительность теперь не является основным определяющим фактором, особенно с приходом мультисэмплинга. Значит, необходимы не только шейдеры, мультисэмплинг и трехмерные текстуры, но и что-то кардинально новое, способное стать существенным аргументом в пользу покупки карт на R200, даже при более высокой цене. Аргумент нашелся — это новая технология ATI, получившая имя "TRUFORM". Основу этой технологии составляет новое представление и методика тесселяции гладких поверхностей, так называемые N-Patches и, что самое главное, поддержка всего этого на аппаратном уровне в R200:
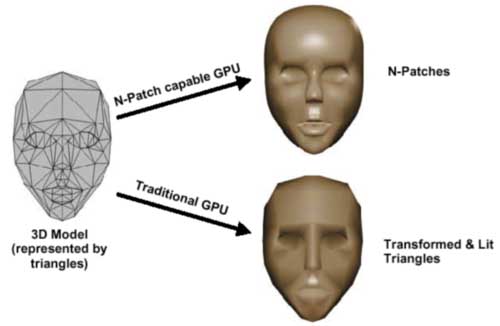
давайте посмотрим на схему, которая позволит нам сразу выделить отличия от описанных ранее прямоугольных патчей:

Новый алгоритм тесселяции разбивает на регулируемое число треугольников не прямоугольную поверхность, а треугольник (!) с заранее заданным для каждой точки вектором нормали.
Для того, чтобы пропущенная через подобных тесселятор полигональная модель оставалась гладкой, без щелей, необходимо обеспечить стыковку краев, получаемых из каждого треугольника поверхностей. Для этого, кривая, описывающая край, должна полностью определяться только координатами двух ограничивающих ее точек и соответствующими им значениями нормали. Давайте посмотрим, как происходит разбиение треугольника и как достигается бесшовная стыковка. Для каждой вершины треугольника строятся две (по числу прилегающих сторон) контрольных точки. Каждая из них вычисляется следующим образом:

Здесь N1 — вектор нормали, P1 — вершина, получаемая контрольная точка b210 относится к точке P1 и ребру P1-P2. Точка лежит в пересечении плоскости, проходящей через вершину перпендикулярно нормали и через ребро, параллельно нормали, на расстоянии одной трети длины ребра. Вычислив, кроме того, одну центральную контрольную точку, мы получаем следующий набор (10 точек включая вершины):
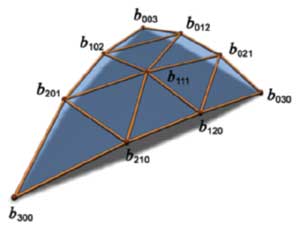
Отметим, что средняя контрольная точка вычисляется несколько иным образом. Затем, задаваемая этими контрольными точками гладкая поверхность тесселируется до необходимого уровня и степени гладкости. Итак, края стыкуются, и с увеличением уровня тесселяции модель становится все более гладкой:

Но не забудем, что нам еще необходимо вычислить координаты нормалей для вновь создаваемых точек. Они получаются путем линейной интерполяции (по поверхности) нормалей исходных вершин. Например, для самого слабого разбиения, где мы получаем 4 треугольника вместо одного, наблюдается следующая картина:
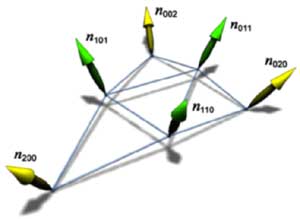
Вектор нормали вновь созданной на грани точки является просто полусуммой векторов вершин соответствующей грани. Разумеется, подобным образом надо интерполировать не только нормали, но и все атрибуты вершин, например координаты привязки текстур или цвет, значения прозрачности, тумана и пр. Кроме того, в R200 есть режим повышенного качества — в нем интерполяция параметров выполняется более сложно, но и результат более точно соответствует геометрической кривизне поверхности. Т.е., фактически, сетка, по которой линейно интерполируют параметры, содержит втрое больше треугольников, нежели будет выведено при отрисовки. Для каждого рисуемого после тесселяции треугольника находятся промежуточные значения параметров на середине его сторон, и уже между ними и вершинами проводится линейная интерполяция.
Давайте посмотрим на результаты применения этой технологии к геометрии хорошо знакомой модели из DX8 SDK:
Результат налицо. А самое главное, формат задания модели совершенно не изменился! Все, что нам надо — это старая, заданная треугольниками модель, векторы нормали в каждой точки и определиться с желаемой глубиной тесселяции. Более того, и с точки зрения программирования мы в большом выигрыше. Код отрисовки во многих случаях просто останется прежним — достаточно один раз проинициализировать использование N-патчей, установить глубину тесселяции и выдавать на отрисовку треугольники стандартным образом, наблюдая, как они аппаратно превращаются в гладкие поверхности.
Впрочем, здесь есть один подводный камень. Многие приложения используют для расчета освещения не векторы нормалей, а карты освещения или какие-либо иные техники, поставляя уже рассчитанные значения цвета для вершин. В таком случае прекрасный результат гарантирован лишь для геометрии, но отнюдь не для закраски и текстурирования. Действительное преимущество получат те приложения, которые работают со стандартными источниками света и возможностями T&L — понадобится внести в них лишь минимальные изменения для поддержки новой технологии. Форсирование N-Patches на уровне драйверов также теоретически возможно (для программ, созданных ранее, и не знающих об этой технологии) однако хороший результат можно гарантировать лишь в случае незатейливого построения сцены, причем вновь лишь с использованием стандартной модели освещения с заданием нормалей и источников света. Возможно, что игры со сложным многопроходным построением сцены (например, Unreal), применяющие процедурные текстуры и карты освещения будут не играбельны в подобном форсированном режиме из-за большого количества различных визуальных артефактов. Что-ж, подождем — увидим…
На данный момент технология N-Pathces поддерживается DirectX 8 и пропиретарным расширением OpenGL принадлежащим Ati, т.е. доступна во всех основных API. Аппаратная поддержка на данный момент присутствует только у R200.
Итого
К достоинствам технологии TRUFORM от ATi относятся все ранее перечисленные плюсы при задании моделей в виде кривых поверхностей. Напомним:
- В случае аппаратной реализации тесселирования резко снижается нагрузка на AGP и шину памяти — мы храним и передаем небольшое количество геометрической информации, а в результате получаем детальную поверхность из множества треугольников.
- Легко реализовать отрисовку моделей, заданных подобным образом, с адаптивным (в зависимости от расстояния до модели) уровнем детализации — мы просто меняем число треугольников, на которое ускоритель разбивает сегмент.
- Мы полностью задействуем мощь современных ускорителей и, в первую очередь, их T&L блоки, не упираясь в слабый центральный процессор системы.
- Большое число треугольников позволяет организовать освещение и тени без использования карт освещения, полностью переложив заботы об оном на шейдеры и T&L. Подобный подход позволит создать невероятную динамическую среду — все предметы будут отбрасывать тени, все источники света смогут двигаться по произвольным траекториям. Исчезнет необходимость в длительных предварительных расчетах.
В тоже время, треугольные сегменты (N-Patches), используемые в технологии TRUFORM, избавляют нас ото всех (!) ранее перечисленных недостатков. Ну, а некоторые из них волшебным образом превращаются в достоинства:
- Все модели задаются единым образом вне зависимости от наличия аппаратной поддержки этой технологии, т.е. "арт" игры не требует переработки и каких-либо специальных условий создания.
- Необходимая для поддержки этой технологии модификация кода минимальна. Сам код отрисовки (вывода), как правило, остается нетронутым, необходимо лишь вовремя включать и выключать соответствующую возможность.
- Потенциальная возможность форсирования этой технологии на уровне драйверов (под вопросом)
- Поддержка DirectX 8 и OpenGL
Осталось лишь дождаться первых карт на базе R200 и проверить на практике, как работает TRUFORM.




