• Конференция
  • Поиск
    • Обзоры
    • Новости
    • Блоги
    Статьи Новости

    Алгоритмы шифрования ? финалисты конкурса AES. Часть 2



    Алгоритм MARS

    Алгоритм MARS был разработан коллективом криптологов из корпорации IBM. Именно IBM в свое время разработала семейство алгоритмов Lucifer, которое легло в основу прошлого стандарта шифрования США — DES. Из авторов Lucifer в разработке алгоритма MARS принял участие Дон Копперсмит (Don Coppersmith), известный также и другими работами в области криптологии.

    По правилам конкурса AES разрешалось вносить незначительные изменения в участвовавшие в конкурсе алгоритмы в течение первого раунда конкурса. Пользуясь этим правилом, авторы алгоритма MARS изменили процедуру расширения ключа, в результате чего существенно снизились требования, предъявляемые алгоритмом к энергонезависимой и оперативной памяти [13]. Рассмотрим здесь именно модифицированную версию алгоритма.

    Структура алгоритма

    Исходя из двух следующих предположений [6]:

    1. Многие известные криптоаналитические методы отличают первый и последний раунды алгоритма (или несколько первых и/или несколько последних раундов) от остальных и применяют к ним другие приемы, нежели к «центральным» раундам алгоритма. Таким образом, различные раунды алгоритма шифрования играют различное значение в обеспечиваемой алгоритмом криптостойкости.
    2. Скорее всего, алгоритм с гетерогенной структурой будет лучше противостоять криптоаналитическим методам будущего, чем алгоритм, все раунды которого идентичны.

    - разработчики алгоритма MARS придали ему сильно гетерогенную структуру — раунды алгоритма весьма различаются между собой. Алгоритм MARS можно описать следующим образом (см. рис. 6):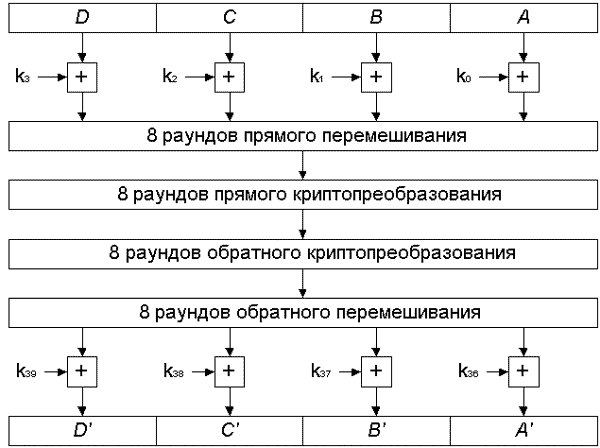Структура алгоритма MARS

    Рис. 6. Структура алгоритма MARS.
    1. Предварительное наложение ключа: на 32-битные субблоки A, B, C, D накладываются 4 фрагмента расширенного ключа k0...k3 операцией сложения по модулю 232.
    2. Выполняются 8 раундов прямого перемешивания (без участия ключа шифрования).
    3. Выполняются 8 раундов прямого криптопреобразования.
    4. Выполняются 8 раундов обратного криптопреобразования. Этапы 3 и 4 называются «криптографическим ядром» алгоритма MARS.
    5. Выполняются 8 раундов обратного перемешивания, также без участия ключа шифрования.
    6. Финальное наложение фрагментов расширенного ключа k36...k39 операцией вычитания по модулю 232.

    Алгоритм представляет собой расширенную сеть Фейстеля. В каждом раунде выполняется обработка одного из субблоков и наложение результатов обработки на остальные субблоки, после чего субблоки меняются местами. Конкретные преобразования зависят от типа раунда и будут рассмотрены ниже. Кроме того, между раундами могут выполняться различные дополнительные действия, которые также будут описаны далее.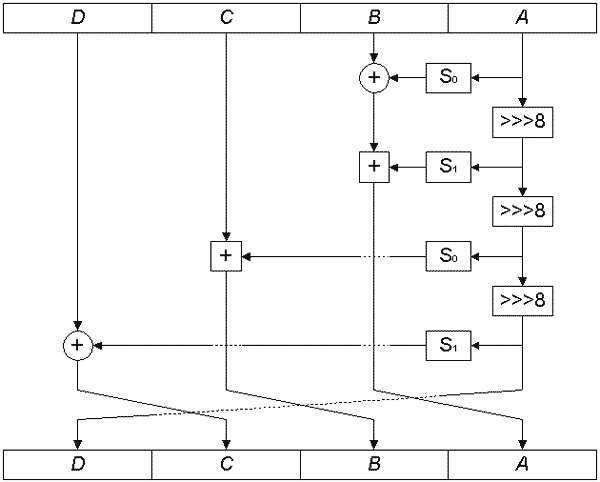Раунд прямого перемешивания алгоритма MARS

    Рис. 7. Раунд прямого перемешивания алгоритма MARS.

    Раунд прямого перемешивания показан на рис. 7. Как видно из рисунка, в раунде выполняются следующие действия:

    1. Значение субблока A прогоняется через таблицу замен S0 и накладывается на субблок B операцией XOR.
    2. Исходное значение субблока A вращается на 8 бит вправо.
    3. Результат предыдущего шага обрабатывается таблицей замен S1 и снова накладывается на субблок B операцией сложения по модулю 232.
    4. Результат шага 2 вращается на 8 бит вправо.
    5. Результат предыдущего шага обрабатывается таблицей замен S0 и накладывается на субблок С операцией сложения по модулю 232.
    6. Результат шага 4 вращается на 8 бит вправо.
    7. Результат предыдущего шага обрабатывается таблицей замен S1 и накладывается на субблок D операцией XOR.
    8. Субблоки меняются местами, как показано на рис. 7.

    Кроме того, в некоторых раундах прямого перемешивания выполняются следующие дополнительные операции (не приведены на рис. 7):

    1. В раундах 0 и 4 после шага 7 выполняется наложение значения субблока D на субблок A операцией сложения по модулю 232.
    2. В раундах 1 и 5 субблок B аналогичным образом накладывается на субблок A.

    По словам авторов алгоритма, эти операции существенно усиливают алгоритм MARS против дифференциального криптоанализа.

    Таблицы замен S0 и S1 определены в спецификации алгоритма [6] следующим образом:

    S0:

    09D0C47928C8FFE084AA6C399DAD72877DFF9BE3D4268361
    C96DA1D47974CC9385D0582E2A4B57051CA16A62C3BD279D
    0F1F25E55160372FC695C1FB4D7FF1E4AE5F6BF40D72EE46
    FF23DE8AB1CF8E83F14902E23E981E428BF53EB67F4BF8AC
    83631F832597020576AFE7843A7931D44F8464505C64C3F6
    210A5F18C6986A2628F4E8263A60A81CD340A6647EA820C4
    526687C57EDDD12B32A11D1D9C9EF08680F6E831AB6F04AD
    56FB9B538B2E095CB68556AED2250B0D294A7721E21FB253
    AE136749E82AAE869336510499404A6678A784DCB69BA84B
    0404679323DB5C1E46CAE1D62FE281345A2239421863CD5B
    C190C6E307DFB8466EB888162D0DCC4AA4CCAE593798670D
    CBFA94934F481D45EAFC5CA5DB1129D6B0449E200F5407FB
    6167D9A8D1F457634DAA96C33BEC5958ABABA014B6CCD201
    38D6279F026822158F376CD5092C237EBFC5659332889D2C
    854B3E9505BB5B437DCD5DCDA02E926CFAE527E536A1C330
    3412E1AEF257F4623C4F1D7130A2E80968E5F5519C61BA44
    5DED0AB875CE09C89654F93E698C0CCA243CB3E42B062B97
    0F3B8D9E00E050DFFC5D6166E35F9288C079550D0591AEE8
    8E531E7475FE35782F6D829AF60B21AE95E8EB8D6699486B
    901D7D9BFD6D6E311090ACEFE0670DD8DAB2E692CD6D4365
    E53935143AF345F06241FC4D460DA3A37BCF37295BF1D1E0
    14AAC0701587ED553AFD7D3ED2F29E0129A9D1F6EFB10C53
    CF3B870FB414935C664465ED024ACAC759A744C11D2936A7
    DC580AA6CF574CA8040A7A106CD818078A98BE4CAССЕА063
    C33E92B5D1E0E03DB322517E2092BD13386B2C4A52E8DD58
    58656DFB5082037141811896E337EF7ED39FB119C97F0DF6
    68FEA01BA150A6E555258962EB6FF41BD7C9CD7AA619CD9E
    BCF095762672C073F003FB3C4AB7A50B1484126A487BA9B1
    A64FC9C6F6957D4938B06A75DD805FCD63D094CFF51C999E
    1AA4D343B8495294CE9F8E99BFFCD770C7C275CC378453A7
    7B21BE33397F41BD4E94D13192CC1F985915EA5199F861B7
    C9980A881D74FD5FB0A495F8614DEED0B5778EEA5941792D
    FA90C1F833F824B4C49653723FF6D5504CA5FEC08630E964
    5B3FBBD67DA26A48B203231A042975142D6393062EB13149
    16A45272532459A08E5F4872F966C7D907128DC00D44DB62
    AFC8D52D06316131D838E7CE1BC41D003A2E8C0FEA83837E
    B984737D13BA4891C4F8B949A6D6ACB3A215CDCE8359838B
    6BD1AA31F579DD5221B93F93F5176781187DFDDEE94AEB76
    2B38FD54431DE1DAAB3948259AD3048FDFEA32AA659473E3
    623F7863F3346C59AB3AB6853346A90B6B56443EC6DE01F8
    8D421FC09B0ED10C88F1A1E954C1F0297DEAD57B8D7BA426
    4CF5178A551A7CCA1A9A5F08FCD651B925605182E11FC6C3
    B6FD9676337B3027B7C8EB149E5FD030  

    В качестве входного значения S0 (аналогично и S1) принимает 8 младших бит входного слова. Таблица меняет значение 0 на 09D0C479, значение 1 — на 28C8FFE0 и т. д.

    S1:

    6B57E354AD913CF77E16688D58872A692C2FC7DFE389CCC6
    30738DF10824A734E1797A8BA4A8D57B5B5D193BC8A8309B
    73F9A97873398D320F59573EE9DF2B03E8A5B6C8848D0704
    98DF93C2720A1DC3684F259A943BA848A6370152863B5EA3
    D17B978B6D9B58EF0A700DD4A73D36BF8E6A08298695BC14
    E35B3447933AC5688894B0222F511C27DDFBCC3C006662B6
    117C83FE4E12B414C2BCA7663A2FEC10F456242055792E2A
    46F5D857CEDA25CEC3601D3B6C00AB46EFAC9C28B3C35047
    611DFEE3257C3207FDD584823B14D84F23BECB64A075F3A3
    088F8EAD07ADF1587796943CFACABF3DC09730CDF7679969
    DA44E9ED2C854C1235935FA32F057D9F690624F81CB0BAFD
    7B0DBDC6810F23BBFA929A1A6D969A176742979B74AC7D05
    010E65C486A3D963F907B5A0D0042BD3158D7D03287A8255
    BBA8366F096EDC3321916A7B77B56B86951622F9A6C5E650
    8CEA17D1CD8C62BCA3D63433358A68FD0F9B9D3CD6AA295B
    FE33384AC000738ECD67EB2FE2EB6DC297338B0206C9F246
    419CF1AD2B83C0453723F18ACB5B3089160BEAD75D494656
    35F8A74B1E4E6C9E000399BD67466880B4174831ACF423B2
    CA815AB35A6395E7302A67C58BDB446B108F8FA410223EDA
    92B8B48B7F38D0EEAB2701D40262D415AF224A30B3D88ABA
    F8B2C3AFDAF7EF70CC97D3B7E9614B6C2BAEBFF470F687CF
    386C9156CE092EE501E87DA66CE91E6ABB7BCC84C7922C20
    9D3B71FD060E41C6D7590F154E03BB47183C198E63EEB240
    2DDBF49A6D5CBA54923750AFF9E142367838162B59726C72
    81B66760BB2926C148A0CE0DA6C0496DAD43507B718D496A
    9DF057AF44B1BDE6054356DCDE7CED35D51A138B62088CC9
    35830311C96EFCA2686F86EC8E77CB6863E1D6B8C80F9778
    79C491FD1B4C67F272698D7D5E368C31F7D95E2EA1D3493F
    DCD9433E896F15524BC4CA7AA6D1BAF4A5A96DCC0BEF8B46
    A169FDA774DF40B74E2088049A756607038E87C820211E44
    8B7AD4BFC6403F351848E36D80BDB0381E62891C643D2107
    BF04D6F821092C8CF644F3890778404E7B78ADB8A2C52D53
    42157ABEA2253E2E7BF3F4AE80F594F9953194E777EB92ED
    B3816930DA8D9336BF447469F26D9483EE6FAED571371235
    DE425F73B4E59F437DBE2D4E2D37B18549DC9A6398C39D98
    1301C9A2389B1BBF0C18588DA421C1BA7AA3865C71E08558
    3C5CFCAA7D239CA40297D9DDD7DC28304B37802B7428AB54
    AEEE03474B3FBB85692F2F08134E578E36D9E0BFAE8B5FCF
    EDB93ECF2B27248E170EB1EF7DC57FD61E760F16B1136601
    864E1B9BD7EA73193AB871BDCFA4D76FE31BD7820DBEB469
    ABB960615370F85DFFB07E37DA50D0FBEBC977B60B98B40F
    3A4D0FE6DF4FC26B159CF22AC298D6E22B78EF6A61A94AC0
    AB56118714EEA0F0DF0D416419AF70EE  

    Структура раунда прямого криптопреобразования приведена на рис. 8.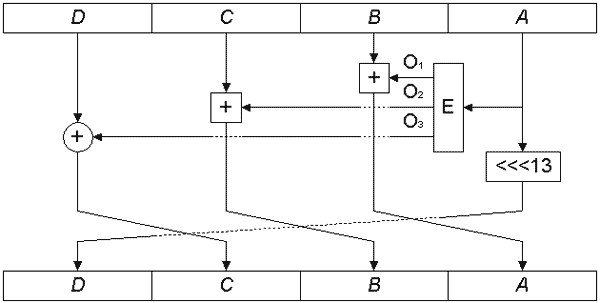Раунд прямого криптопреобразования алгоритма MARS

    Рис. 8. Раунд прямого криптопреобразования алгоритма MARS.

    Основой раунда является расширяющее криптопреобразование E, преобразующее 32-битное входное слово A в три выходных 32-битных значения, каждое из которых определенным образом накладывается на остальные субблоки (см. рис. 8). После этого субблок A вращается влево на 13 бит, затем субблоки меняются местами аналогично раунду прямого перемешивания.

    Преобразование E показано на рис. 9.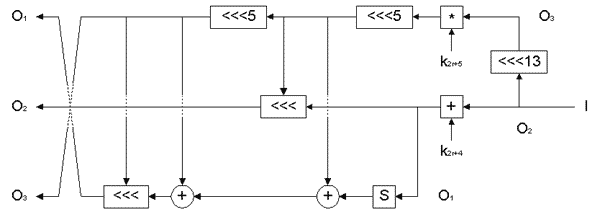Операция E алгоритма MARS

    Рис. 9. Операция E алгоритма MARS.
    Щёлкните по картинке, чтобы увеличить.

    Из входного значения формируются три потока O1...O3, над которыми производятся следующие действия:

    O2 = I,
    O3 = O2 <<< 13,
    O2 = O2 + k2r+4 mod 232,
    O3 = O3 * k2r+5 mod 232,
    O3 = O3 <<< 5,
    O1 = S(O2),
    O1 = O1 Å O3,
    O2 = O2 <<< O3’,
    O3 = O3 <<< 5,
    O1 = O1 Å O3,
    O1 = O1 <<< O3’,

    где I — входное значение,
    r — номер текущего раунда, считая с 0-го (при нумерации раундов в данном случае учитываются только раунды криптоядра алгоритма),
    S — табличная замена для операции E, представляет собой объединение описанных выше таблиц S0 и S1; объединенная таблица содержит 512 значений, выходное значение выбирается по значению 9 младших бит входного слова.

    Стоит обратить внимание на то, что в преобразовании E используются операции вращения на переменное число бит; в этом случае запись O3’ обозначает, что число бит вращения определяется значением младших пяти бит текущего значения O3.

    Структура обратного криптораунда показана на рис. 10.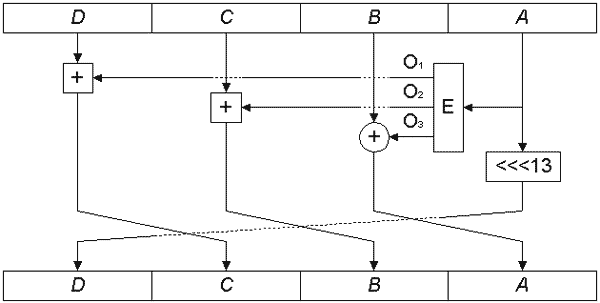Раунд обратного криптопреобразования алгоритма MARS

    Рис. 10. Раунд обратного криптопреобразования алгоритма MARS.

    От прямого криптораунда его отличает лишь измененный порядок наложения выходных значений преобразования E O1...O3 на слова B, C и D.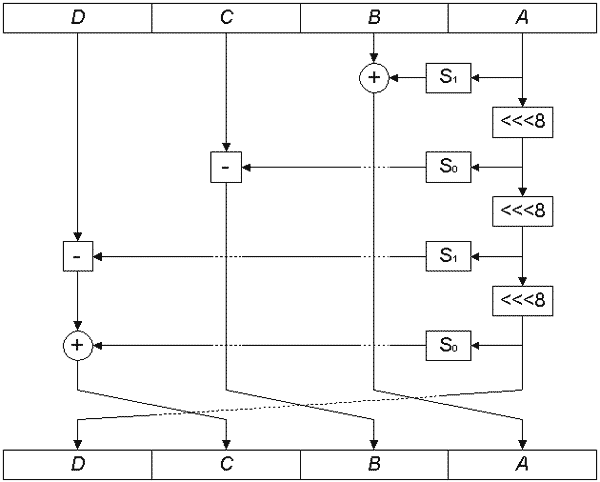Раунд обратного перемешивания алгоритма MARS

    Рис. 11. Раунд обратного перемешивания алгоритма MARS.

    Раунд обратного перемешивания (см. рис. 11) более существенно отличается от прямого. Фактически, обратное перемешивание выполняет обратные операции в обратной последовательности (см. рис. 7 и 11):

    1. Значение субблока A прогоняется через таблицу замен S1 и накладывается на субблок B операцией XOR.
    2. Исходное значение субблока A вращается на 8 бит влево.
    3. Результат предыдущего шага обрабатывается таблицей замен S0 и накладывается на субблок C операцией вычитания по модулю 232.
    4. Результат шага 2 вращается на 8 бит влево.
    5. Результат предыдущего шага обрабатывается таблицей замен S1 и накладывается на субблок D операцией вычитания по модулю 232.
    6. Результат шага 4 вращается на 8 бит влево.
    7. Результат предыдущего шага обрабатывается таблицей замен S0 и накладывается на субблок D операцией XOR.
    8. Субблоки меняются местами, как показано на рис. 11.

    Аналогично прямому перемешиванию, в некоторых раундах выполняются следующие дополнительные операции, не показанные на рис. 11:

    1. В раундах 1 и 5 после шага 7 выполняется наложение значения субблока A на субблок B операцией вычитания по модулю 232.
    2. В раундах 2 и 6 субблок C аналогичным образом накладывается на субблок B.

    Расшифрование выполняется применением обратных операций в обратной последовательности; подробно расшифрование описано в спецификации алгоритма [6].

    Процедура расширения ключа

    Ключ шифрования алгоритма MARS может иметь любой размер в диапазоне от 128 до 448 бит включительно, кратный 32 битам. Расширение ключа представляет собой формирование на основе ключа шифрования 40 подключей по 32 бита каждый (причем, подключи должны обладать определенными характеристиками, о которых будет сказано ниже), для чего выполняются следующие операции:

    1. Формируется временный массив T0...T14:

      T0 = KI0,
      T1 = KI1,
      ...
      Tn-1 = KIn-1,
      Tn = n,
      Tn+1 = Tn+2 = ... = T14 = 0,

      где KI0...KIn-1 — исходный ключ шифрования,
      n — его размер в 32-битных словах — от 4 до 14 включительно.

    2. Данный шаг повторяется 4 раза (каждая итерация дает 10 вычисленных фрагментов расширенного ключа) и содержит следующие операции:
      • линейное преобразование:
        Ti = Ti Å ((Ti-7 mod 15 Å Ti-2 mod 15) <<< 3) Å (4i + j),
        где j — номер итерации, начиная с 0,
        i = 0...14;
      • перемешивание массива T:
        Ti = (Ti Å S(Ti-1 mod 15)) <<< 9,
        где S — табличная замена, выполняемая по тем же правилам, что и в операции E;
      • заключительная перестановка:
        k10j+n = T4n mod15,
        где n = 0...9.
    3. Наложение на вычисленные подключи дополнительных требований, состоящих в следующем:
      1. Каждый подключ, используемый для умножения в операции E (то есть подключи с нечетными индексами от k5 до k35 включительно), должен иметь нечетное значение. Мало того, единичными должны быть два младших бита подключа, а не один.
      2. Те же подключи не должны содержать 10 нулевых или 10 единичных бит подряд.
      Модификация подключей в соответствии с данными требованиями выполняется следующим образом:
      1. 2 младших бита обрабатываемого подключа устанавливаются в единичные значения; старое значение запоминается в переменной j (оно будет использовано впоследствии). Результирующее значение подключа обозначается как W.
      2. Вычисляется 32-битная маска M, которая будет использована для модификации подключа — для обеспечения отсутствия в нем 10 подряд нулевых или единичных бит. Маска вычисляется следующим образом:
        A) Устанавливаются в 1 биты M, соответствующие тем битам обрабатываемого подключа, которые входят в последовательности из 10 нулевых или 10 единичных бит. Остальные биты устанавливаются в 0.
        B) Обнуляются те единичные биты маски M, которые соответствуют любому из условий:
        i < 2,
        i = 31,
        Wi != Wi-1,
        Wi != Wi+1,
        где i — номер бита, начиная с 0, а Wi — значение i-го бита.
      3. Используется таблица корректирующих значений B, определенная следующим образом:
        B0 = A4A8D57B,
        B1 = 5B5D193B,
        B2 = C8A8309B,
        B3 = 73F9A978.

        Элементы таблицы B эквивалентны элементам с 265-го по 268-й включительно объединенной таблицы S; именно эти элементы используются для коррекции подключей благодаря их специфическим свойствам.
        С помощью данной таблицы следующим образом вычисляется финальное значение подключа Ki:
        Ki = W Å ((Bj <<< Ki-1) & M),
        где & — логическая побитовая операция «и», а вращение Bj определяется пятью младшими битами предыдущего подключа Ki-1.

    Описанная процедура гарантирует требуемые свойства у подключей [6].Алгоритм RC6

    Алгоритм RC6 был разработан в 1998 г. рядом специалистов научного подразделения известнейшей фирмы RSA Data Security — RSA Laboratories: Рональдом Ривестом (Ronald Rivest, основатель RSA Data Security), Мэттом Робшоу (Matt Robshaw), Рэем Сидни (Ray Sidney) и Икван Лайзой Ин (Yiqun Lisa Yin) специально для участия в конкурсе AES [17]. Алгоритм во многом унаследовал черты предыдущего алгоритма Рональда Ривеста — 64-битного блочного шифра RC5, разработанного в 1997 г. (подробное описание RC5 на русском языке можно найти в [19]). Фактически, алгоритм претерпел два принципиальных изменения:

    • в отличие от RC5, в алгоритме используется умножение по модулю 232;
    • для сохранения 32-битных вычислений вместо разбиения шифруемого блока данных (128 бит согласно принципиальному требованию конкурса AES) на два 64-битных субблока выполняется его разбиение на 4 32-битных субблока и их обработка по несколько измененной схеме [17].

    Структура алгоритма

    Как и алгоритм RC5, RC6 имеет гибкую структуру: помимо секретного ключа, параметрами алгоритма являются следующие:

    • размер слова w; RC6 шифрует блоками по 4 слова;
    • количество раундов алгоритма R;
    • размер секретного ключа в байтах b.

    Аналогично RC5, для уточнения параметров алгоритма, используемых в его конкретной реализации, применяется обозначение RC6-w/R/b. Поскольку в конкурсе AES 128-битный блок является обязательным, значение w фиксировано и равно 32. В спецификации алгоритма [14] фиксируется также количество раундов: R = 20. Поскольку конкурс AES предусматривает использование трех фиксированных размеров ключей, рассмотрим три следующих варианта алгоритма: RC6-32/20/16, RC6-32/20/24 и RC6-32/20/32, совокупность которых и будет подразумеваться далее под названием «RC6».

    Структура алгоритма представлена на рис. 12.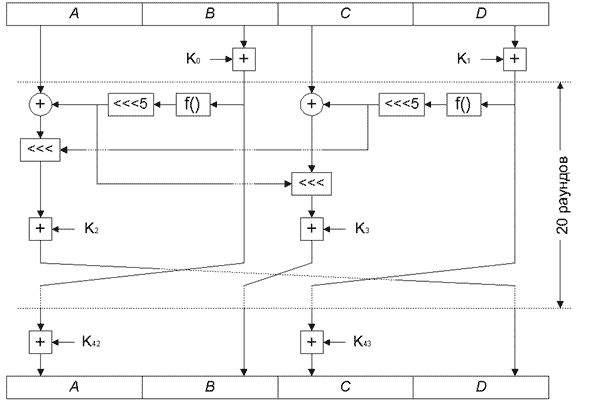Структура алгоритма RC6

    Рис. 12. Структура алгоритма RC6.
    Щёлкните по картинке, чтобы увеличить.

    Как было сказано выше, в алгоритме используется 20 раундов преобразований, перед которыми выполняется частичное входное отбеливание:

    B = B + K0 mod 232,
    D = D + K1 mod 232,

    где A, B, C, D — текущие значения обрабатываемых 32-битных субблоков,
    K0...K43 — фрагменты расширенного ключа.

    Аналогичным образом выполняется частичное выходное отбеливание:

    A = A + K42 mod 232,
    C = C + K43 mod 232.

    В каждом раунде алгоритма выполняются следующие действия:

    t1 = f(B) <<< 5,
    t2 = f(D) <<< 5,
    A = ((A Å t1) <<< t2) + K2i mod 232,
    C = ((C Å t2) <<< t1) + K2i+1 mod 232,

    где t1 и t2 — временные переменные,
    количество бит вращения на переменное число бит определяется значением 5 младших бит параметра (t1 или t2),
    функция f() выполняет следующее квадратичное преобразование:

    f(x) = x * (2x + 1) mod 232.

    В конце каждого раунда выполняется сдвиг субблоков — см. рис. 12.

    При расшифровании подключи используются в обратном порядке, наложение подключей вместо сложения по модулю 232 выполняется вычитанием, а также сдвиг субблоков выполняется в начале раунда и в обратную сторону. Преобразование f() не претерпело изменений (см. рис. 13).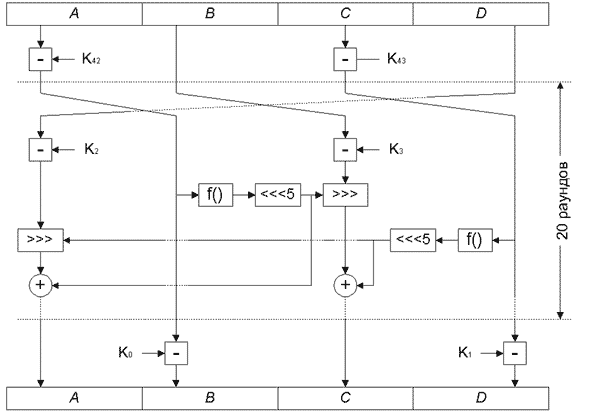Расшифрование алгоритмом RC6

    Рис. 13. Расшифрование алгоритмом RC6.
    Щёлкните по картинке, чтобы увеличить.

    Процедура расширения ключа

    Процедура расширения ключа RC6 аналогична RC5, за исключением того, что RC6 требуется существенно больше сгенерированных подключей, а именно 2R+4, то есть K0...K43 для 20 раундов. Рассмотрим данную процедуру для алгоритма RC6 в варианте для конкурса AES, то есть с указанными выше фиксированными параметрами.

    Расширение ключа выполняется в два этапа:

    1. Инициализация массива расширенных ключей K0...K43, которая производится следующим образом:
      K0 = P32,
      Ki+1 = Ki + Q32 mod 232,
      где P32 и Q32 — псевдослучайные константы, образованные путем умножения на 232 дробной части и последующего округления до ближайшего нечетного целого двух математических констант (e и f соответственно):
      P32 = B7E15163,
      Q32 = 9E3779B9,
      Авторы алгоритма в его спецификации [14] утверждают, что выбор данных значений не является важным. Соответственно, аналогично описанному выше алгоритму Twofish-FK, при необходимости создания реализации алгоритма RC6, не совместимой со стандартной, следует изменить значения P32 и Q32.
    2. Циклически выполняются следующие действия:
      A = Ki = (Ki + A + B mod 232) <<< 3,
      B = KIj = (KIj + A + B mod 232) <<< (A + B),
      i = i + 1 mod 44,
      j = j + 1 mod c,
      где i, j, A и B — временные переменные, их начальные значения равны нулю,
      KI — исходный ключ шифрования, представленный в виде c 32-битных слов.
      Выполняется 3c итераций цикла.
    Достоинства и недостатки алгоритмов-финалистов

    Результаты проделанной аналитиками работы по изучению алгоритмов-финалистов NIST сформулировал в виде отчета [12]. Данный отчет содержит как результаты анализа алгоритмов, так и обоснование критериев, по которым выполнялась оценка. Автор данной статьи позволил себе на основе отчета [12] кратко сформулировать сравнительные оценки пяти алгоритмов-финалистов конкурса AES по основным критериям в виде следующей таблицы:

    №КатегорияSerpentTwofishMARSRC6Rijndael
    1Криптостойкость+++++
    2Запас криптостойкости++++++++
    3Скорость шифрования при программной реализации-±±++
    4Скорость расширения ключа при программной реализации±-±±+
    5Смарт-карты с большим объемом ресурсов++-±++
    6Смарт-карты с ограниченным объемом ресурсов±+-±++
    7Аппаратная реализация (ПЛИС)++-±+
    8Аппаратная реализация (специализированная микросхема)+±--+
    9Защита от атак по времени выполнения и потребляемой мощности3+±--+
    10Защита от атак по потребляемой мощности на процедуру расширения ключа±±±±-
    11Защита от атак по потребляемой мощности на реализации в смарт-картах±+-±+
    12Возможность расширения ключа «на лету»++±±±
    13Наличие вариантов реализации (без потерь в совместимости)++±±+
    14Возможность параллельных вычислений±±±±+

    Стоит прокомментировать некоторые строки приведенной таблицы:

    1. Криптостойкость всех алгоритмов-финалистов оказалась достаточной — в процессе исследований не было обнаружено каких-либо реально реализуемых атак на полноценные и полнораундовые версии алгоритмов. В данном случае криптоаналитики обычно исследуют варианты алгоритмов с усеченным числом раундов, либо с некоторыми внесенными изменениями, незначительными, но ослабляющими алгоритм. Под запасом криптостойкости (security margin) эксперты NIST подразумевают соотношение полного (предусмотренного в спецификациях алгоритмов) числа раундов и максимального из тех вариантов, против которых действуют какие-либо криптоаналитические атаки. Например, с помощью дифференциально-линейного криптоанализа вскрывается 11-раундовый Serpent [5], тогда как в оригинальном алгоритме выполняется 32 раунда. Эксперты NIST в отчете [12] предупредили, что данная оценка является весьма поверхностной и не может быть значимой при выборе алгоритма-победителя конкурса, но, тем не менее, отметили, что запас криптостойкости у Rijndael и RC6 несколько ниже, чем у остальных алгоритмов-финалистов.
    2. В пп. 5-8 приведена сравнительная оценка возможности и эффективности реализации алгоритмов в перечисленных устройствах.
    3. В пп. 9-11 имеется в виду, насколько операции, выполняемые конкретным алгоритмом, могут быть подвержены анализу указанным методом. При этом принималось в расчет то, что операции могут быть модифицированы с целью усложнения криптоанализа за счет потери в скорости шифрования (например, проблемное в этом смысле вращение на переменное число бит может принудительно выполняться за равное число тактов — то есть максимально возможное для данной операции; именно подобные меры противодействия атакам по времени исполнения и потребляемой мощности рекомендует их изобретатель Пол Кохер (Paul C. Kocher) [11]).
    4. Из описаний алгоритмов видно, что все они поддерживают расширение ключа «на лету» (то есть подключи могут генерироваться непосредственно в процессе шифрования — по мере необходимости), однако, только Serpent и Twofish поддерживают такую возможность без каких-либо ограничений.
    5. Под наличием вариантов реализации (implementation flexibility) имеется в виду возможность различным образом реализовывать какие-либо операции алгоритма с оптимизацией под конкретные цели. Наиболее показательными в этом смысле являются упомянутые ранее варианты процедуры расширения ключа алгоритма Twofish [16], позволяющие оптимизировать реализацию алгоритма в зависимости, прежде всего, от частоты смены ключа.

    Сформулируем основные достоинства и недостатки каждого из рассмотренных в данной статье алгоритмов-финалистов [12]:

    АлгоритмДостоинстваНедостатки
    Serpent
    1. Простая структура алгоритма облегчает его анализ с целью нахождения возможных уязвимостей.
    2. Serpent эффективно реализуем аппаратно и в условиях ограниченных ресурсов.
    3. Serpent легко модифицируется с целью защиты от атак по времени выполнения и потребляемой мощности (однако, за счет снижения скорости).
    1. Является самым медленным из алгоритмов-финалистов в программных реализациях.
    2. Процедуры зашифрования и расшифрования абсолютно различны, т.е. требуют раздельной реализации.
    3. Распараллеливание вычислений при шифровании алгоритмом Serpent реализуемо с ограничениями.
    Twofish
    1. Twofish эффективно реализуем аппаратно и в условиях ограниченных ресурсов.
    2. Зашифрование и расшифрование в алгоритме Twofish практически идентичны.
    3. Является лучшим из алгоритмов-финалистов с точки зрения поддержки расширения ключа «на лету».
    4. Несколько вариантов реализации позволяют оптимизировать алгоритм для конкретных применений.
    1. Сложность структуры алгоритма затрудняет его анализ.
    2. Сложная и медленная процедура расширения ключа.
    3. Относительно сложно защищается от атак по времени выполнения и потребляемой мощности.
    4. Распараллеливание вычислений при шифровании алгоритмом Twofish реализуемо с ограничениями.
    MARSЗашифрование и расшифрование в алгоритме MARS практически идентичны.
    1. Исключительно сложная структура алгоритма с раундами различных типов затрудняет как анализ алгоритма, так и его реализацию.
    2. Возникают проблемы при программной реализации на тех платформах, которые не поддерживают 32-битное умножение и вращение на переменное число бит.
    3. Алгоритм MARS не может быть эффективно реализован аппаратно и в условиях ограниченных ресурсов.
    4. Сложно защищается от атак по времени выполнения и потребляемой мощности.
    5. MARS хуже других алгоритмов-финалистов поддерживает расширение ключей «на лету».
    6. Распараллеливание вычислений при шифровании алгоритмом MARS реализуемо с ограничениями.
    RC6
    1. Простая структура алгоритма облегчает его анализ. Кроме того, алгоритм унаследовал часть преобразований от своего предшественника — алгоритма RC5, тщательно проанализированного до конкурса AES.
    2. Самый быстрый из алгоритмов-финалистов на 32-битных платформах.
    3. Зашифрование и расшифрование в алгоритме RC6 практически идентичны.
    1. Скорость шифрования при программной реализации сильно зависит от того, поддерживает ли платформа 32-битное умножение и вращение на переменное число бит.
    2. RC6 сложно реализуем аппаратно и в условиях ограниченных ресурсов.
    3. Достаточно сложно защищается от атак по времени выполнения и потребляемой мощности.
    4. Недостаточно полно поддерживает расширение ключей «на лету».
    5. Распараллеливание вычислений при шифровании алгоритмом RC6 реализуемо с ограничениями.
    Заключение

    Как известно, проанализировав результаты всех исследований, эксперты выбрали в качестве стандарта AES алгоритм Rijndael. Что не выглядит удивительным — в таблице с характеристиками алгоритмов отчетливо видно, что практически по всем характеристикам Rindael, как минимум, не уступает остальным алгоритмам-финалистам.

    Что касается алгоритмов Serpent, Twofish, MARS и RC6, то видно, что они практически равнозначны по совокупности характеристик, за исключением алгоритма MARS, имеющего существенно больше недостатков, в том числе, алгоритм практически нереализуем в условиях ограниченных ресурсов.Литература, источники

    1. AES Round 1 Information. // http://csrc.nist.gov — January 26, 2001.
    2. Anderson R., Biham E. Two Practical and Provably Secure Block Ciphers: BEAR and LION. // http://citeseer.ist.psu.edu — 1995.
    3. Anderson R., Biham E., Knudsen L. Serpent: A Proposal for the Advanced Encryption Standard. // http://csrc.nist.gov.
    4. Announcing Request for Candidate Algorithm Nominations for the Advanced Encryption Standard (AES). // http://csrc.nist.gov — Department of Commerce — National Institute of Standards and Technology — Federal Register: September 12, 1997.
    5. Biham E., Dunkelman O., Keller N. Differential-Linear Cryptanalysis of Serpent. // http://citeseer.ist.psu.edu — Technion, Haifa, Israel.
    6. Burwick C., Coppersmith D., D’Avignon E., Gennaro R., Halevi S., Jutla C., Matyas S.M.Jr., O’Connor L., Peyravian M., Safford D., Zunic N. MARS — a candidate cipher for AES. // http://www.ibm.com — IBM Corporation — Revised, September, 22 1999.
    7. Courtois N., Castagnos G., Goubin L. What do DES S-boxes Say to Each Other? // http://eprint.iacr.org — Axalto Cryptographic Research & Advanced Security, Cedex, France.
    8. Daemen J., Knudsen L., Rijmen V. The Block Cipher Square. // http://www.esat.kuleuven.ac.be.
    9. FIPS 46-3. Data Encryption Standard (DES). // http://csrc.nist.gov — Reaffirmed 1999 October 25.
    10. FIPS 81. DES Modes of Operation. // http://csrc.nist.gov — 1980 December 2.
    11. Kocher P.C. Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. // http://citeseer.ist.psu.edu — Cryptography Research, Inc., San Francisco, USA.
    12. Nechvatal J., Barker E., Bassham L., Burr W., Dworkin M., Foti J., Roback E. Report on the Development of the Advanced Encryption Standard (AES). // http://csrc.nist.gov — National Institute of Standards and Technology.
    13. Nechvatal J., Barker E., Dodson D., Dworkin M., Foti J., Roback E. Status report on the first round of the development of the advanced encryption standard. // http://csrc.nist.gov — National Institute of Standards and Technology.
    14. Rivest R.L., Robshaw M.J.B., Sidney R., Lin Y.L. The RC6 Block Cipher. // http://www.rsasecurity.com — Version 1.1 — August 20, 1998.
    15. Schneier B. Description of a new variable-length key 64-bit block cipher (blowfish). // http://www.schneier.com.
    16. Schneier B., Kelsey J., Whiting D., Wagner D., Hall C., Ferguson N. Twofish: A 128-bit Block Cipher. // http://www.schneier.com — 15 June 1998.
    17. What are RC5 and RC6? // http://www.rsasecurity.com.
    18. Панасенко С. Алгоритм шифрования DES и его варианты. // Connect! Мир связи. — 2006 — №№ 3-6.
    19. Панасенко С. Интересные алгоритмы шифрования, часть 2. // BYTE/Россия. — 2006 — № 5 — с. 74-79.
    20. Панасенко С.П., Батура В.П. Основы криптографии для экономистов: учебное пособие. Под ред. Л.Г. Гагариной. — М.: Финансы и статистика, 2005 — 176 с.
    21. Соколов А.В., Шаньгин В.Ф. Защита информации в распределенных корпоративных сетях и системах. — М.: ДМК Пресс, 2002 — 656 с.
    22. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. — Пер. с англ.: М.: Издательство ТРИУМФ, 2002 — 816 с.


    25 августа 2006 Г.

    AES. 2.

    — AES. 2


    MARS

    MARS IBM. IBM Lucifer, — DES. Lucifer MARS (Don Coppersmith), .

    AES . , MARS , , [13]. .

    [6]:

    1. ( / ) , . , .
    2. , , , .

    - MARS — . MARS (. . 6):

    MARS
    . 6. MARS.
    1. : 32- A, B, C, D 4 k0...k3 232.
    2. 8 ( ).
    3. 8 .
    4. 8 . 3 4 MARS.
    5. 8 , .
    6. k36...k39 232.

    . , . . , , .

    MARS
    . 7. MARS.

    . 7. , :

    1. A S0 B XOR.
    2. A 8 .
    3. S1 B 232.
    4. 2 8 .
    5. S0 232.
    6. 4 8 .
    7. S1 D XOR.
    8. , . 7.

    , ( . 7):

    1. 0 4 7 D A 232.
    2. 1 5 B A.

    , MARS .

    S0 S1 [6] :

    S0:

    09D0C47928C8FFE084AA6C399DAD72877DFF9BE3D4268361
    C96DA1D47974CC9385D0582E2A4B57051CA16A62C3BD279D
    0F1F25E55160372FC695C1FB4D7FF1E4AE5F6BF40D72EE46
    FF23DE8AB1CF8E83F14902E23E981E428BF53EB67F4BF8AC
    83631F832597020576AFE7843A7931D44F8464505C64C3F6
    210A5F18C6986A2628F4E8263A60A81CD340A6647EA820C4
    526687C57EDDD12B32A11D1D9C9EF08680F6E831AB6F04AD
    56FB9B538B2E095CB68556AED2250B0D294A7721E21FB253
    AE136749E82AAE869336510499404A6678A784DCB69BA84B
    0404679323DB5C1E46CAE1D62FE281345A2239421863CD5B
    C190C6E307DFB8466EB888162D0DCC4AA4CCAE593798670D
    CBFA94934F481D45EAFC5CA5DB1129D6B0449E200F5407FB
    6167D9A8D1F457634DAA96C33BEC5958ABABA014B6CCD201
    38D6279F026822158F376CD5092C237EBFC5659332889D2C
    854B3E9505BB5B437DCD5DCDA02E926CFAE527E536A1C330
    3412E1AEF257F4623C4F1D7130A2E80968E5F5519C61BA44
    5DED0AB875CE09C89654F93E698C0CCA243CB3E42B062B97
    0F3B8D9E00E050DFFC5D6166E35F9288C079550D0591AEE8
    8E531E7475FE35782F6D829AF60B21AE95E8EB8D6699486B
    901D7D9BFD6D6E311090ACEFE0670DD8DAB2E692CD6D4365
    E53935143AF345F06241FC4D460DA3A37BCF37295BF1D1E0
    14AAC0701587ED553AFD7D3ED2F29E0129A9D1F6EFB10C53
    CF3B870FB414935C664465ED024ACAC759A744C11D2936A7
    DC580AA6CF574CA8040A7A106CD818078A98BE4CA063
    C33E92B5D1E0E03DB322517E2092BD13386B2C4A52E8DD58
    58656DFB5082037141811896E337EF7ED39FB119C97F0DF6
    68FEA01BA150A6E555258962EB6FF41BD7C9CD7AA619CD9E
    BCF095762672C073F003FB3C4AB7A50B1484126A487BA9B1
    A64FC9C6F6957D4938B06A75DD805FCD63D094CFF51C999E
    1AA4D343B8495294CE9F8E99BFFCD770C7C275CC378453A7
    7B21BE33397F41BD4E94D13192CC1F985915EA5199F861B7
    C9980A881D74FD5FB0A495F8614DEED0B5778EEA5941792D
    FA90C1F833F824B4C49653723FF6D5504CA5FEC08630E964
    5B3FBBD67DA26A48B203231A042975142D6393062EB13149
    16A45272532459A08E5F4872F966C7D907128DC00D44DB62
    AFC8D52D06316131D838E7CE1BC41D003A2E8C0FEA83837E
    B984737D13BA4891C4F8B949A6D6ACB3A215CDCE8359838B
    6BD1AA31F579DD5221B93F93F5176781187DFDDEE94AEB76
    2B38FD54431DE1DAAB3948259AD3048FDFEA32AA659473E3
    623F7863F3346C59AB3AB6853346A90B6B56443EC6DE01F8
    8D421FC09B0ED10C88F1A1E954C1F0297DEAD57B8D7BA426
    4CF5178A551A7CCA1A9A5F08FCD651B925605182E11FC6C3
    B6FD9676337B3027B7C8EB149E5FD030  

    S0 ( S1) 8 . 0 09D0C479, 1 — 28C8FFE0 . .

    S1:

    6B57E354AD913CF77E16688D58872A692C2FC7DFE389CCC6
    30738DF10824A734E1797A8BA4A8D57B5B5D193BC8A8309B
    73F9A97873398D320F59573EE9DF2B03E8A5B6C8848D0704
    98DF93C2720A1DC3684F259A943BA848A6370152863B5EA3
    D17B978B6D9B58EF0A700DD4A73D36BF8E6A08298695BC14
    E35B3447933AC5688894B0222F511C27DDFBCC3C006662B6
    117C83FE4E12B414C2BCA7663A2FEC10F456242055792E2A
    46F5D857CEDA25CEC3601D3B6C00AB46EFAC9C28B3C35047
    611DFEE3257C3207FDD584823B14D84F23BECB64A075F3A3
    088F8EAD07ADF1587796943CFACABF3DC09730CDF7679969
    DA44E9ED2C854C1235935FA32F057D9F690624F81CB0BAFD
    7B0DBDC6810F23BBFA929A1A6D969A176742979B74AC7D05
    010E65C486A3D963F907B5A0D0042BD3158D7D03287A8255
    BBA8366F096EDC3321916A7B77B56B86951622F9A6C5E650
    8CEA17D1CD8C62BCA3D63433358A68FD0F9B9D3CD6AA295B
    FE33384AC000738ECD67EB2FE2EB6DC297338B0206C9F246
    419CF1AD2B83C0453723F18ACB5B3089160BEAD75D494656
    35F8A74B1E4E6C9E000399BD67466880B4174831ACF423B2
    CA815AB35A6395E7302A67C58BDB446B108F8FA410223EDA
    92B8B48B7F38D0EEAB2701D40262D415AF224A30B3D88ABA
    F8B2C3AFDAF7EF70CC97D3B7E9614B6C2BAEBFF470F687CF
    386C9156CE092EE501E87DA66CE91E6ABB7BCC84C7922C20
    9D3B71FD060E41C6D7590F154E03BB47183C198E63EEB240
    2DDBF49A6D5CBA54923750AFF9E142367838162B59726C72
    81B66760BB2926C148A0CE0DA6C0496DAD43507B718D496A
    9DF057AF44B1BDE6054356DCDE7CED35D51A138B62088CC9
    35830311C96EFCA2686F86EC8E77CB6863E1D6B8C80F9778
    79C491FD1B4C67F272698D7D5E368C31F7D95E2EA1D3493F
    DCD9433E896F15524BC4CA7AA6D1BAF4A5A96DCC0BEF8B46
    A169FDA774DF40B74E2088049A756607038E87C820211E44
    8B7AD4BFC6403F351848E36D80BDB0381E62891C643D2107
    BF04D6F821092C8CF644F3890778404E7B78ADB8A2C52D53
    42157ABEA2253E2E7BF3F4AE80F594F9953194E777EB92ED
    B3816930DA8D9336BF447469F26D9483EE6FAED571371235
    DE425F73B4E59F437DBE2D4E2D37B18549DC9A6398C39D98
    1301C9A2389B1BBF0C18588DA421C1BA7AA3865C71E08558
    3C5CFCAA7D239CA40297D9DDD7DC28304B37802B7428AB54
    AEEE03474B3FBB85692F2F08134E578E36D9E0BFAE8B5FCF
    EDB93ECF2B27248E170EB1EF7DC57FD61E760F16B1136601
    864E1B9BD7EA73193AB871BDCFA4D76FE31BD7820DBEB469
    ABB960615370F85DFFB07E37DA50D0FBEBC977B60B98B40F
    3A4D0FE6DF4FC26B159CF22AC298D6E22B78EF6A61A94AC0
    AB56118714EEA0F0DF0D416419AF70EE  

    . 8.

    MARS
    . 8. MARS.

    E, 32- A 32- , (. . 8). A 13 , .

    E . 9.

    E MARS
    . 9. E MARS.
    ٸ , .

    O1...O3, :

    O2 = I,
    O3 = O2 <<< 13,
    O2 = O2 + k2r+4 mod 232,
    O3 = O3 * k2r+5 mod 232,
    O3 = O3 <<< 5,
    O1 = S(O2),
    O1 = O1 Å O3,
    O2 = O2 <<< O3,
    O3 = O3 <<< 5,
    O1 = O1 Å O3,
    O1 = O1 <<< O3,

    I — ,
    r — , 0- ( ),
    S — E, S0 S1; 512 , 9 .

    , E ; O3 , O3.

    . 10.

    MARS
    . 10. MARS.

    E O1...O3 B, C D.

    MARS
    . 11. MARS.

    (. . 11) . , (. . 7 11):

    1. A S1 B XOR.
    2. A 8 .
    3. S0 C 232.
    4. 2 8 .
    5. S1 D 232.
    6. 4 8 .
    7. S0 D XOR.
    8. , . 11.

    , , . 11:

    1. 1 5 7 A B 232.
    2. 2 6 C B.

    ; [6].

    MARS 128 448 , 32 . 40 32 (, , ), :

    1. T0...T14:

      T0 = KI0,
      T1 = KI1,
      ...
      Tn-1 = KIn-1,
      Tn = n,
      Tn+1 = Tn+2 = ... = T14 = 0,

      KI0...KIn-1 — ,
      n — 32- — 4 14 .

    2. 4 ( 10 ) :
      • :
        Ti = Ti Å ((Ti-7 mod 15 Å Ti-2 mod 15) <<< 3) Å (4i + j),
        j — , 0,
        i = 0...14;
      • T:
        Ti = (Ti Å S(Ti-1 mod 15)) <<< 9,
        S — , , E;
      • :
        k10j+n = T4n mod15,
        n = 0...9.
    3. , :
      1. , E ( k5 k35 ), . , , .
      2. 10 10 .
      :
      1. 2 ; j ( ). W.
      2. 32- M, — 10 . :
        A) 1 M, , 10 10 . 0.
        B) M, :
        i < 2,
        i = 31,
        Wi != Wi-1,
        Wi != Wi+1,
        i — , 0, Wi — i- .
      3. B, :
        B0 = A4A8D57B,
        B1 = 5B5D193B,
        B2 = C8A8309B,
        B3 = 73F9A978.

        B 265- 268- S; .
        Ki:
        Ki = W Å ((Bj <<< Ki-1) & M),
        & — , Bj Ki-1.

    [6].

    RC6

    RC6 1998 . RSA Data Security — RSA Laboratories: (Ronald Rivest, RSA Data Security), (Matt Robshaw), (Ray Sidney) (Yiqun Lisa Yin) AES [17]. — 64- RC5, 1997 . ( RC5 [19]). , :

    • RC5, 232;
    • 32- (128 AES) 64- 4 32- [17].

    RC5, RC6 : , :

    • w; RC6 4 ;
    • R;
    • b.

    RC5, , , RC6-w/R/b. AES 128- , w 32. [14] : R = 20. AES , : RC6-32/20/16, RC6-32/20/24 RC6-32/20/32, RC6.

    . 12.

    RC6
    . 12. RC6.
    ٸ , .

    , 20 , :

    B = B + K0 mod 232,
    D = D + K1 mod 232,

    A, B, C, D — 32- ,
    K0...K43 — .

    :

    A = A + K42 mod 232,
    C = C + K43 mod 232.

    :

    t1 = f(B) <<< 5,
    t2 = f(D) <<< 5,
    A = ((A Å t1) <<< t2) + K2i mod 232,
    C = ((C Å t2) <<< t1) + K2i+1 mod 232,

    t1 t2 — ,
    5 (t1 t2),
    f() :

    f(x) = x * (2x + 1) mod 232.

    — . . 12.

    , 232 , . f() (. . 13).

    RC6
    . 13. RC6.
    ٸ , .

    RC6 RC5, , RC6 , 2R+4, K0...K43 20 . RC6 AES, .

    :

    1. K0...K43, :
      K0 = P32,
      Ki+1 = Ki + Q32 mod 232,
      P32 Q32 — , 232 (e f ):
      P32 = B7E15163,
      Q32 = 9E3779B9,
      [14] , . , Twofish-FK, RC6, , P32 Q32.
    2. :
      A = Ki = (Ki + A + B mod 232) <<< 3,
      B = KIj = (KIj + A + B mod 232) <<< (A + B),
      i = i + 1 mod 44,
      j = j + 1 mod c,
      i, j, A B — , ,
      KI — , c 32- .
      3c .

    -

    - NIST [12]. , , . [12] - AES :

    SerpentTwofishMARSRC6Rijndael
    1+++++
    2 ++++++++
    3 -±±++
    4 ±-±±+
    5- ++-±++
    6- ±+-±++
    7 ()++-±+
    8 ( )+±--+
    9 3+±--+
    10 ±±±±-
    11 -±+-±+
    12 ++±±±
    13 ( )++±±+
    14 ±±±±+

    :

    1. - — - . , , , . (security margin) NIST ( ) , - . , - 11- Serpent [5], 32 . NIST [12] , - , , , , Rijndael RC6 , -.
    2. . 5-8 .
    3. . 9-11 , , , . , (, — ; (Paul C. Kocher) [11]).
    4. , ( — ), , Serpent Twofish - .
    5. (implementation flexibility) - . Twofish [16], , , .

    - [12]:

    Serpent
    1. .
    2. Serpent .
    3. Serpent (, ).
    1. - .
    2. , .. .
    3. Serpent .
    Twofish
    1. Twofish .
    2. Twofish .
    3. - .
    4. .
    1. .
    2. .
    3. .
    4. Twofish .
    MARS MARS .
    1. , .
    2. , 32- .
    3. MARS .
    4. .
    5. MARS - .
    6. MARS .
    RC6
    1. . , — RC5, AES.
    2. - 32- .
    3. RC6 .
    1. , 32- .
    2. RC6 .
    3. .
    4. .
    5. RC6 .

    , , AES Rijndael. — , Rindael, , -.

    Serpent, Twofish, MARS RC6, , , MARS, , , .

    ,

    1. AES Round 1 Information. // http://csrc.nist.gov — January 26, 2001.
    2. Anderson R., Biham E. Two Practical and Provably Secure Block Ciphers: BEAR and LION. // http://citeseer.ist.psu.edu — 1995.
    3. Anderson R., Biham E., Knudsen L. Serpent: A Proposal for the Advanced Encryption Standard. // http://csrc.nist.gov.
    4. Announcing Request for Candidate Algorithm Nominations for the Advanced Encryption Standard (AES). // http://csrc.nist.gov — Department of Commerce — National Institute of Standards and Technology — Federal Register: September 12, 1997.
    5. Biham E., Dunkelman O., Keller N. Differential-Linear Cryptanalysis of Serpent. // http://citeseer.ist.psu.edu — Technion, Haifa, Israel.
    6. Burwick C., Coppersmith D., DAvignon E., Gennaro R., Halevi S., Jutla C., Matyas S.M.Jr., OConnor L., Peyravian M., Safford D., Zunic N. MARS — a candidate cipher for AES. // http://www.ibm.com — IBM Corporation — Revised, September, 22 1999.
    7. Courtois N., Castagnos G., Goubin L. What do DES S-boxes Say to Each Other? // http://eprint.iacr.org — Axalto Cryptographic Research & Advanced Security, Cedex, France.
    8. Daemen J., Knudsen L., Rijmen V. The Block Cipher Square. // http://www.esat.kuleuven.ac.be.
    9. FIPS 46-3. Data Encryption Standard (DES). // http://csrc.nist.gov — Reaffirmed 1999 October 25.
    10. FIPS 81. DES Modes of Operation. // http://csrc.nist.gov — 1980 December 2.
    11. Kocher P.C. Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. // http://citeseer.ist.psu.edu — Cryptography Research, Inc., San Francisco, USA.
    12. Nechvatal J., Barker E., Bassham L., Burr W., Dworkin M., Foti J., Roback E. Report on the Development of the Advanced Encryption Standard (AES). // http://csrc.nist.gov — National Institute of Standards and Technology.
    13. Nechvatal J., Barker E., Dodson D., Dworkin M., Foti J., Roback E. Status report on the first round of the development of the advanced encryption standard. // http://csrc.nist.gov — National Institute of Standards and Technology.
    14. Rivest R.L., Robshaw M.J.B., Sidney R., Lin Y.L. The RC6 Block Cipher. // http://www.rsasecurity.com — Version 1.1 — August 20, 1998.
    15. Schneier B. Description of a new variable-length key 64-bit block cipher (blowfish). // http://www.schneier.com.
    16. Schneier B., Kelsey J., Whiting D., Wagner D., Hall C., Ferguson N. Twofish: A 128-bit Block Cipher. // http://www.schneier.com — 15 June 1998.
    17. What are RC5 and RC6? // http://www.rsasecurity.com.
    18. . DES . // Connect! . — 2006 — 3-6.
    19. . , 2. // BYTE/. — 2006 — 5 — . 74-79.
    20. .., .. : . . .. . — .: , 2005 — 176 .
    21. .., .. . — .: , 2002 — 656 .
    22. . . , , . — . .: .: , 2002 — 816 .


    25 2006 , http://www.panasenko.ru

    Новости

    Раздел новостей >
    Попробовать новый дизайн       Подробнее

    Copyright © 1997—2024.

    О сайте

    Адрес для связи info@ixbt.com

    Наши проекты
    Полезные ссылки
    Связь с администрацией

    Нашли ошибку? Выделите текст и нажмите Shift+Enter.

    Copyright © 1997-2024